Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Sau 0,5 s từ thời điểm ban đầu vật đi được quãng đường
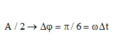
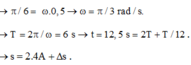
Trong khoảng thời gian T/12 s từ thời điểm ban đầu vật đi được quãng đường A/2
Từ phương trình ta thấy ban đầu vật đang ở biên độ âm (-5cm).
Do vậy để vật đi được quãng đường S=5cm kể từ thời điểm ban đầu, thì vật đi từ biên độ âm về vị trí cân bằng. Thời gian này bằng 1/4 chu kì dao động.
\(t=\dfrac{1}{4}.\dfrac{2\pi}{10\pi}=\dfrac{1}{20}s\)
Chọn D
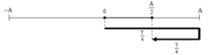
+ Lúc t = 0: xo = 0 và vo > 0 => để đi được s= 3 cm => đi đến x = 3 = A/2 => t1 = T/12 = 0,5 => T = 6 (s).
+ t2 = 20,5 (s) = 3T + 5T/12=> s = 3.4A + Δs (Δs là quãng đường đi thêm trong 5T/12).
+ Vì vật xuất phát ở xo = 0 và vo > 0 nên tách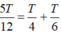 
=> Δs = A + A/2 = 1,5A.
+ Vậy, tổng quãng đường trong thời gian t2 là: s = 3/4A + 1,5A = 81 (cm).
Chu kì: T = 1s.
Thời gian: t = 2,4s = 2T + 0,4T.
+ Trong thời gian 2T quãng đường đi được là: S1 = 2.4A = 2.4.5 = 40cm.
+ Trong thời gian 0,4T véc tơ quay đã quay một góc 0,4. 360 = 1440
5 -5 -2,5 M1 M2 120 24
Quãng đường vật đã đi trong thời gian này: S2 = 2,5 + 5 + (5 - 5.cos240) = 7,9cm
Vậy tổng quãng đường vật đi: 40 + 7,9 = 47,9cm.
Biểu diễn dao động bằng véc tơ quay:
x 4 -4 -2 M N O 30°
Ban đầu, véc tơ quay xuất phát ở M, để dao động đi được 6cm thì véc tơ quay sẽ quay đến N.
Trên hình vẽ ta tìm được góc quay là: \(\alpha=90+30=120^0\)
Thời gian: \(t=\dfrac{120}{360}T=\dfrac{\pi}{30}\)
\(\Rightarrow T=\dfrac{\pi}{10} (s)\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Cơ năng của vật: \(W=\dfrac{1}{2}.m.\omega^2.A^2=\dfrac{1}{2}.1.20^2.0,04^2=0,32(J)\)
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)
Từ thời điểm t = 0 đến t = 0,5s bằng đúng 1 chu kì nên quãng đường vật đi được là: \(4A=4.6=24cm\)
