Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 7: Đổi 30 phút=\(\frac{1}{2}h\)
Gọi quãng đường cần đi là S ( tính theo km, và S>0 )
Khi đó thời gian dự định cần đi là:
\(\frac{S}{30}\)(h)
Thời gian đi nửa quãng đường trước là:
\(\frac{S}{2}\): 30 =\(\frac{S}{60}\)(h)
Thời gian đi nửa quãng đường sau là:
\(\frac{S}{2}:40=\frac{S}{80}\)(h)
Do thời gian giảm đi 30 phút nên:
\(\frac{S}{60}+\frac{S}{80}+\frac{1}{2}=\frac{S}{30}\)
<=> \(\frac{S}{240}=\frac{1}{2}\)
<=> S= 120 (km)
Vậy quãng đường cần tìm là 120 km

\(\dfrac{A}{B}=\dfrac{3x^4+3x^2+x^3+x-3x^2-3+5x-2}{x^2+1}=3x^2+x-3+\dfrac{5x-2}{x^2+1}\)
Để A chia hết cho B thì \(\left(5x-2\right)\left(5x+2\right)⋮x^2+1\)
\(\Leftrightarrow25x^2-4⋮x^2+1\)
\(\Leftrightarrow25x^2+25-29⋮x^2+1\)
\(\Leftrightarrow x^2+1\in\left\{1;29\right\}\)
hay \(x\in\left\{0;2\sqrt{7};-2\sqrt{7}\right\}\)

Câu 2/ \(\dfrac{157}{68}=2+\dfrac{21}{68}=2+\dfrac{1}{\dfrac{68}{21}}\)
\(=2+\dfrac{1}{3+\dfrac{5}{21}}=2+\dfrac{1}{3+\dfrac{1}{\dfrac{21}{5}}}\)
\(=2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{5}}}\)
Vậy \(\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)

3.
- Gọi x(km) là quãng đường AB ( x > 0 )
- Thời gian đi:\(\dfrac{x}{60}\) (h)
- Thời gia về:\(\dfrac{x}{50}\) (h)
Ta có phương trình
\(\dfrac{x}{50}\) - \(\dfrac{x}{60}\) = \(\dfrac{4}{5}\)
\(\Leftrightarrow\) 6x - 5x = 240
\(\Leftrightarrow\) x = 240 (TM)
Vậy quãng đường AB là 240km

A B E C F
a) Xét \(\Delta\)EBA và \(\Delta\)ABC có:
\(\widehat{BEA}=\widehat{BAC}\left(=90^o\right)\)
\(\widehat{B}\) là góc chung
\(\Rightarrow\) \(\Delta\)EBA đòng dạng vs \(\Delta\)ABC (g - g)
\(\Rightarrow\) \(\dfrac{BE}{AB}=\dfrac{AB}{BC}\)
\(\Rightarrow\) AB2 = BE . BC
b) Trong \(\Delta\)ABC vuông tại A có:
BC2 = AB2 + AC2
= 32 . 42
= 25
\(\Rightarrow\) BC = \(\sqrt{25}\) = 5(cm)
Vì: AB2 = BC.BE (cmt)
\(\Rightarrow\) BE = \(\dfrac{AB^2}{BC}\)
= \(\dfrac{3^2}{5}\) = 1.8(cm)
Xét \(\Delta\)BEA vuông tại E có:
AE2 = AB2 + BE2
= 32 + 1.82
= \(\dfrac{306}{25}\)
\(\Rightarrow\)AE = \(\sqrt{\dfrac{306}{25}}\) = \(\dfrac{3\sqrt{34}}{5}\)(cm)
c) Trong \(\Delta\)ABC có BF là tia phân giác của góc B
\(\Rightarrow\) \(\dfrac{AF}{AB}=\dfrac{CF}{BC}\)
Áp dụng t/chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{AF}{AB}=\dfrac{CF}{BC}\)\(=\dfrac{AF+CF}{AB+BC}=\dfrac{AC}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AF}{3}=\dfrac{1}{2}\Rightarrow AF=1.5\left(cm\right)\)
Trong \(\Delta\)ABF vuông tại A có:
BF2 = AB2 + AF2
= 32 + 1.52
= 11.25
\(\Rightarrow\) BF = \(\sqrt{11.25}\) = \(\dfrac{3\sqrt{5}}{2}\)(cm)

Câu 1:
a: Xét ΔABC vuông tại B và ΔAHB vuông tại H có
góc HAB chung
DO đo:ΔABC đồng dạng với ΔAHB
XétΔABC vuông tại B có BH là đường cao
nên \(AB^2=AH\cdot AC\)
hay \(DC^2=AH\cdot AC\)
b: Xét ΔHBA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(1\right)\)
Xét ΔHBC vuông tại H có HN là đường cao
nên \(BN\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(BM\cdot BA=BN\cdot BC\)
hay BM/BC=BN/BA
Xét ΔBMN và ΔBCA có
BM/BC=BN/BA
góc B chung
DO đo:ΔBMN đồng dạng với ΔBCA
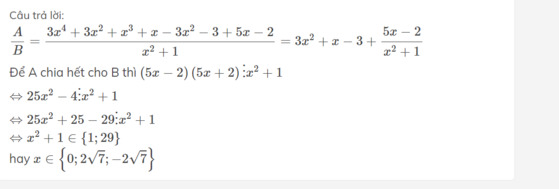
- Gọi vận tốc thực của cano là x ( km/h, x > 0 )
- Vận tốc xuôi dòng là : x + 3 ( km/h )
=> Quãng đường đi là : \(1,5\left(x+3\right)\left(km\right)\)
- Vận tốc ngược dòng là : x - 3 ( km/h )
=> Quãng đường đi là : 2 ( x - 3 ) ( km )
Lại có cả xuôi và ngược đều là quãng đường AB .
=> 2 ( x - 3 ) = 1,5 ( x + 3 )
=> x = 21 ( TM )
Vậy quãng đường AB dài 2. ( 21 - 3 ) = 36 km .
bạn có thể viết rõ phần giải phương trình ra được ko