Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
Giải nhanh giúp mình với nhé mình đang cần gấp
Bài 1 :
\(a,-1\frac{1}{4}+\frac{1}{4}+50\%\)
\(=-\frac{3}{4}+\frac{1}{4}+\frac{1}{2}\)
\(=-\frac{1}{2}+\frac{1}{2}\)
\(=0\)
\(b,0,5+0,5.\left(-80\right).0,01-10\%\)
\(=0,5-40.0,01-10\%\)
\(=0,5-0,4-\frac{1}{10}\)
\(=0,1-\frac{1}{10}\)
\(=\frac{1}{10}-\frac{1}{10}\)
\(=0\)
\(c,\frac{4}{30}\times\frac{2}{5}+\frac{2}{15}\times\frac{4}{5}+\frac{2}{15}\times\left(-\frac{1}{5}\right)\)
\(=\frac{2}{15}\times\frac{2}{5}+\frac{2}{15}\times\frac{4}{5}+\frac{2}{15}\times\left(-\frac{1}{5}\right)\)
\(=\frac{2}{15}\left(\frac{2}{5}+\frac{4}{5}-\frac{1}{5}\right)\)
\(=\frac{2}{15}\times\frac{5}{5}\)
\(=\frac{2}{15}\times1\)
\(=\frac{2}{15}\)
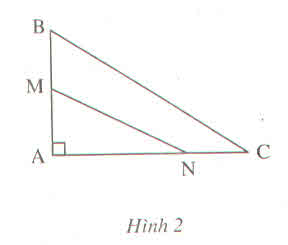
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.
a. ta có :\(\frac{x}{5}=\frac{y}{4}\Rightarrow\frac{x^2}{25}=\frac{y^2}{16}=\frac{x^2-y^2}{25-16}=\frac{9}{9}=1\Rightarrow x^2=25\)
\(\orbr{\begin{cases}x=5\Rightarrow y=4\\x=-5\Rightarrow y=-4\end{cases}}\)
2.\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x^3}{27}=\frac{y^3}{64}=\frac{z^3}{125}=\frac{x^3+y^3-z^3}{27+64-125}=\frac{26}{17}\)
Vậy \(x=3\sqrt[3]{\frac{26}{17}},y=4\sqrt[3]{\frac{26}{17}},z=5\sqrt[3]{\frac{26}{17}}\)
3.\(\frac{x}{\frac{1}{8}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{2}}=\frac{x+y-z}{\frac{1}{8}+\frac{1}{3}-\frac{1}{2}}=-\frac{9}{-\frac{1}{24}}=216\) vậy \(\hept{\begin{cases}x=\frac{216}{8}=27\\y=\frac{216}{3}=72\\z=\frac{216}{2}=108\end{cases}}\)
4.\(\frac{x}{3}=\frac{1-y}{4}=\frac{z}{2}=\frac{3x+1-y-z}{3\times3+4-2}=\frac{11}{11}=1\)
Vậy \(x=3,y=-3,z=2\)
1: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó:ΔABD=ΔACD
2: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
3: Xét ΔMEA vuông tại E và ΔMED vuông tại E có
ME chung
EA=ED
Do đó: ΔMEA=ΔMED
Bài 2
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
b) Xem hình vẽ:
.
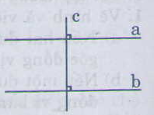
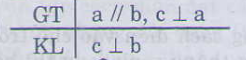Bài 4:
Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau:
GT: a vuông góc với c, b vuông góc với c
KL: a song song với b
Bài 3 chịu
Bài 3:
a) Ta có: \(A-\left(9x^3+8x^2-2x-7\right)=-9x^3-8x^2+5x+11\)
\(\Leftrightarrow A=-9x^3-8x^2+5x+11+9x^3+8x^2-2x-7\)
\(\Leftrightarrow A=3x+4\)
b) Đặt A(x)=0
nên 3x+4=0
hay \(x=-\dfrac{4}{3}\)
Bạn có biết giải bài hình k giúp mình với 21:00 mình phải nộp rồi