Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
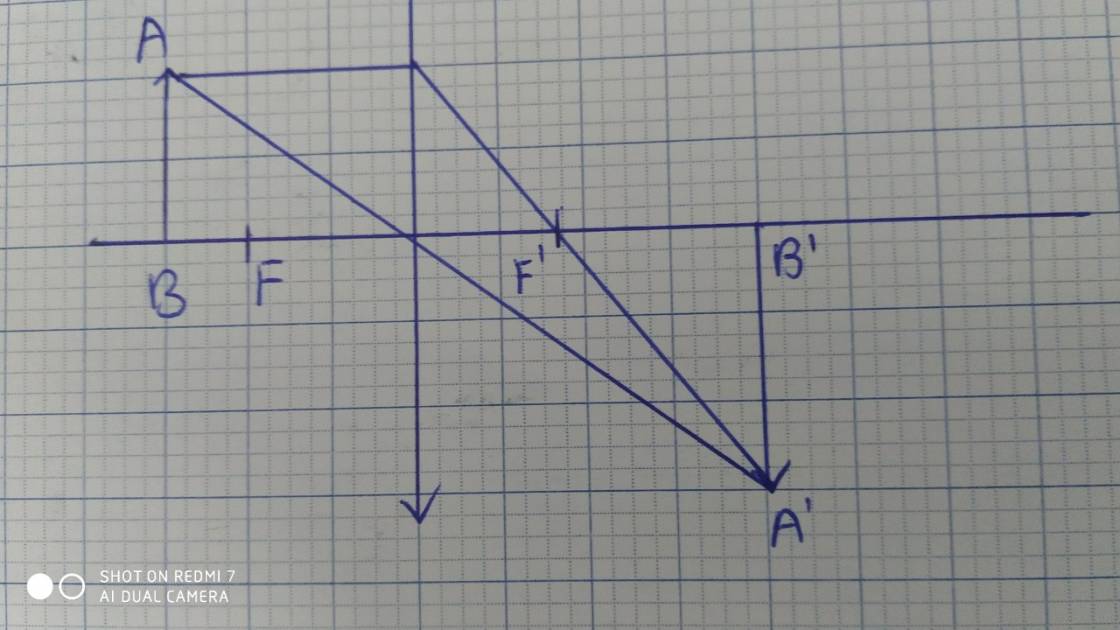
b) Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow\dfrac{d}{h}=\dfrac{d'}{h'}\Leftrightarrow\dfrac{d'}{h'}=\dfrac{20}{2}\Rightarrow d'=10h'\)
Áp dụng công thức thấu kính ta được:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\left(1\right)\)
Thay \(d'=10h'\) vào công thức trên ta có:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{10h'}\) hay \(\dfrac{1}{12}=\dfrac{1}{20}+\dfrac{1}{10h'}\Rightarrow h'=3\left(cm\right)\)
Vậy chiều cao của ảnh là 3cm
Khoảng cách từ màn đến thấu kính:
Ta có: \(d'=10h'=10.3=30cm\)

b)Ảnh thật.
c)Để ảnh thật cao gấp đôi vật \(\Rightarrow h'=2h\) thì:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{2h}=\dfrac{d}{d'}=\dfrac{1}{2}\Rightarrow d'=2d\)
Khi đó vị trí cách thấu kính là:
\(d'=2d=2\cdot50=100cm\)
anh/chị vít lại cái đề ạ
Sửa lại đề roii ạ