K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NG
0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2020
a/ \(log_2\left(2+a\right)=3\Rightarrow2+a=8\Rightarrow a=6\)
b/ Đặt \(\left(2+\sqrt{3}\right)^x=t>0\)
\(\Rightarrow t^2+t=6\Leftrightarrow t^2+t-6=0\Rightarrow\left[{}\begin{matrix}t=-3\left(l\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\left(2+\sqrt{3}\right)^x=2\Rightarrow x=log_{2+\sqrt{3}}2\)
c/ Đặt \(2^x=t>0\)
\(t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2^x=1\\2^x=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
HC
1
RL
1 tháng 3 2016
ĐK;x>0
<=> \(\frac{1}{2}\)log2x-log2x-log52>1
<=>\(\frac{1}{2}\)log2x>1+log52
<=> log2x>\(\frac{1+log_{ }^{ }}{2}\)( ví a=2>0)
<=>x>2\(\frac{1+log_{ }^{ }}{2}\)
RL
1 tháng 3 2016
bài a, nhứ đã giải ở câu trc:
b, ĐK: 0<x, x khác 1.
ta có: log2x64= 6.log2x2= 6( \(\frac{1}{1+log_2x}\))
logx216=2logx2=\(\frac{2}{log_2x}\)
Thay vào pt:
6( \(\frac{1}{1+log_2x}\)) +\(\frac{2}{log_2x}\) =3
đặt T=log2x, ĐK. t>0
<=>6\(\frac{1}{1+t}\) +\(\frac{2}{t}\)=3
.......
<=> t=2( nghiệm -\(\frac{1}{3}\)<0 loại)
.....
<=>x=4(thõa)
CM
7 tháng 2 2019
Chọn C
Điều kiện
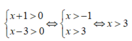
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
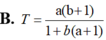
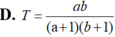
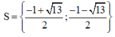
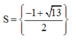
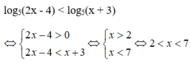
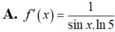
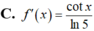
Lời giải:
\(\log_2x+\log_5(x+8)=2\)
\(\Leftrightarrow \log_25.\log_5x+\log_5(x+8)=2\)
\(\Leftrightarrow \log_5(x^{\log_25})+\log_5(x+8)=2\)
\(\Leftrightarrow \log_5(x^{\log_25}(x+8))=2\)
\(\Leftrightarrow x^{\log_25}(x+8)=25\)
PT này mình nghĩ không giải theo kiểu thông thường. Shift-solve thôi ra $x=1,515$