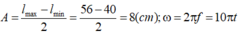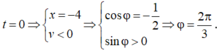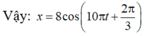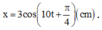Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ban đầu t = 0 thì x = 2 cm, lúc này vật đang ở biên độ dương.
Quả cầu dao động được nửa chu kì thì x = -2 cm (vật ở biên độ âm)
Chiều dài của lò xo: \(\ell=\ell_0+\Delta\ell_0+x=40+10-2=48(cm)\)

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)

\(x=2\sin(\omega t +\dfrac{\pi}{2})=2\cos(\omega t)\) (cm)
Như vậy, ban đầu (t = 0) vật đang ở biên độ dương \(x=2cm\)
Khi quả cầu đi được nửa chu kì dao động thì nó sẽ lên biên độ âm, \(x=-2cm\)
Chiều dài lò xo: \(\ell=\ell_0+\Delta \ell_0+x=40+10-2=48(cm)\)

\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .