Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C5:
\(A=\dfrac{a}{1+b^2c}+\dfrac{b}{1+c^2d}+\dfrac{c}{1+d^2a}+\dfrac{d}{1+a^2b}=\dfrac{a^2}{a+ab^2c}+\dfrac{b^2}{b+bc^2d}+\dfrac{c^2}{c+cd^2a}+\dfrac{d}{d+da^2b}\)
Áp dụng BĐT Cauchy Schwars dạng Engel ta có:
\(A\ge\dfrac{\left(a+b+c+d\right)^2}{a+b+c+d+ab^2c+bc^2d+cd^2a+da^2b}=\dfrac{16}{4+\left(ab+cd\right)\left(bc+ad\right)}\)
\(\ge\dfrac{16}{4+\left(\dfrac{ab+bc+cd+ad}{4}\right)^2}=\dfrac{16}{4+\left[\dfrac{\left(a+c\right)\left(b+d\right)}{2}\right]^2}\ge\dfrac{16}{4+\left[\dfrac{\left(\dfrac{a+b+c+d}{2}\right)^2}{2}\right]^2}=2\)
Dấu ''='' xảy ra khi và chỉ khi a=b=c=d=1

C15. 5:
Áp dụng BĐT Cauchy:
\(\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}+\dfrac{1+b}{8}+\dfrac{1+c}{8}\ge3\sqrt[3]{\dfrac{a^3\left(1+b\right)\left(1+c\right)}{\left(1+b\right)\left(1+c\right).64}}=\dfrac{3a}{4}\)
\(\Rightarrow\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}\ge\dfrac{3a}{4}-\dfrac{b+1}{8}-\dfrac{c+1}{8}\)
Tương tự: \(\Rightarrow\dfrac{b^3}{\left(1+c\right)\left(1+a\right)}\ge\dfrac{3b}{4}-\dfrac{c+1}{8}-\dfrac{a+1}{8}\); \(\Rightarrow\dfrac{c^3}{\left(1+b\right)\left(1+a\right)}\ge\dfrac{3c}{4}-\dfrac{b+1}{8}-\dfrac{a+1}{8}\)
Cộng theo vế: \(VT\ge\dfrac{3}{4}\left(a+b+c\right)-\dfrac{1}{4}\left(a+b+c\right)-\dfrac{3}{4}=\dfrac{a+b+c}{2}-\dfrac{3}{4}\ge\dfrac{3\sqrt[3]{abc}}{2}-\dfrac{3}{4}=\dfrac{3}{4}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=1\)
C15.2: ( Trần Văn Khắnk - Trần Thanh Fuongzz)
Theo định lý Sin: \(\dfrac{a}{sinA}=2R\Rightarrow sinA=\dfrac{a}{2R}\Rightarrow S=\dfrac{1}{2}bc.sinA=\dfrac{abc}{4R}\Leftrightarrow abc=4SR\) (1)
Gọi G là trọng tâm của tam giác ABC, ta có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\Leftrightarrow3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\Leftrightarrow9OG^2=OA^2+OB^2+OC^2+2\overrightarrow{OA}.\overrightarrow{OB}+2\overrightarrow{OB}.\overrightarrow{OC}+2\overrightarrow{OC}.\overrightarrow{OA}\)
\(\Leftrightarrow9OG^2=3R^2+2\overrightarrow{OA}.\overrightarrow{OB}+2\overrightarrow{OB}.\overrightarrow{OC}+2\overrightarrow{OC}.\overrightarrow{OA}\)
Có \(2\overrightarrow{OA}.\overrightarrow{OB}=\overrightarrow{OA}^2+\overrightarrow{OB}^2-\left(\overrightarrow{OA}-\overrightarrow{OB}\right)^2=2R^2-c^2\)
Tương tự suy ra: \(9OG^2=9R^2-\left(a^2+b^2+c^2\right)\Rightarrow a^2+b^2+c^2=9\left(R^2-OG^2\right)\) (2)
Từ (1) và (2), ta có đpcm \(\Leftrightarrow12SR\ge4S\sqrt{9\left(R^2-OG^2\right)}\)
\(\Leftrightarrow R\ge\sqrt{R^2-OG^2}\)
\(\Leftrightarrow OG^2\ge0\) ( luôn đúng )
Dấu "=" xảy ra khi và chỉ khi \(O\equiv G\) hay tam giác ABC đều.

Bài 2.
Ta có:a2+b2+c2+2abc+1≥2(ab+bc+ca)
⇔ (a2-2ab+b2)+(c2-2c+1)+(2c+2abc-2bc-2ca)≥0
⇔ (a-b)2+(c-1)2+2c(a-1)(b-1)≥0
Vì a,b,c≥0 ⇒ 2c(a-1)(b-1)≥0
Dấu "=" xảy ra ⇔ a=b=c=1
C25: b5: Sử dụng kĩ thuật Côsi ngược dấu:
Ta có: \(\dfrac{1}{2bc^2+1}=1-\dfrac{2bc^2}{2bc^2+1}\ge1-\dfrac{2bc^2}{3\sqrt[3]{b^2c^4}}=1-\dfrac{2\sqrt[3]{bc^2}}{3}\)
Cmtt ta được: \(\dfrac{1}{2ca^2+1}\ge1-\dfrac{2\sqrt[3]{ca^2}}{3};\dfrac{1}{2ab^2+1}\ge1-\dfrac{2\sqrt[3]{ab^2}}{3}\)
\(\Rightarrow VT\ge1-\dfrac{2\sqrt[3]{bc^2}}{3}+1-\dfrac{2\sqrt[3]{ca^2}}{3}+1-\dfrac{2\sqrt[3]{ab^2}}{3}=3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)\)
Ta có: Theo bđt Côsi:
\(\sqrt[3]{bc^2}=\sqrt[3]{b.c.c}\le\dfrac{b+c+c}{3}=\dfrac{b+2c}{3}\)
\(\sqrt[3]{ca^2}=\sqrt[3]{c.a.a}\le\dfrac{c+a+a}{3}=\dfrac{c+2a}{3}\)
\(\sqrt[3]{ab^2}=\sqrt[3]{a.b.b}\le\dfrac{a+b+c}{3}=\dfrac{a+2b}{3}\)
\(\Rightarrow\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}\le\dfrac{b+2c+c+2a+a+2b}{3}=a+b+c=3\)
\(\Rightarrow3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)=1\)
\(\Rightarrow VT\ge1\)
Dấu ''='' xảy ra khi a=b=c=1

Cơ hội kiếm thưởng đây! Với quỹ cộng đồng hoc24 lên tới hơn 450.000đ đến hiện tại, giải thưởng giải Nhất đã đạt ở mức 500.000đ!
Nếu các bạn muốn giúp đỡ cộng đồng qua việc đóng góp giải thưởng, hãy chuyển ngay COIN tới tài khoản này nha :>
Xin cảm ơn các nhà hảo tâm:
- Nguyễn Trần Thành Đạt: 400 COIN.
- Sad Boy: 80 COIN.





















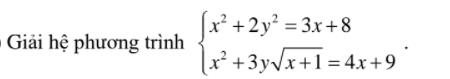
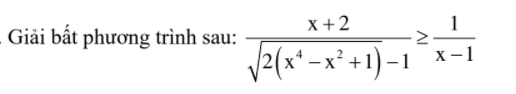
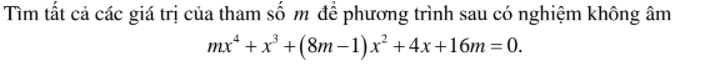

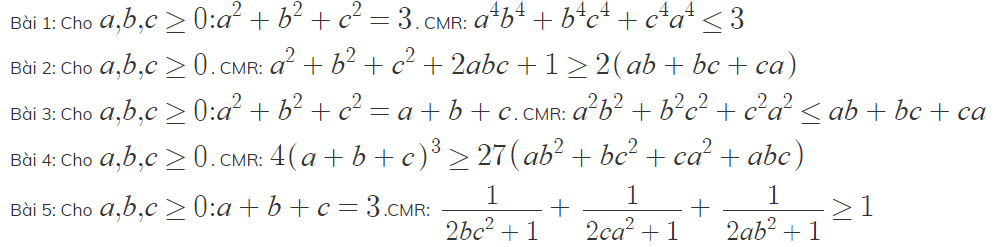
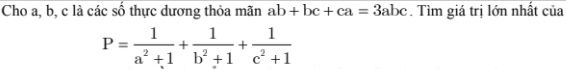
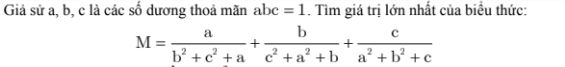




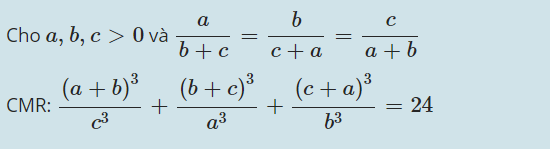
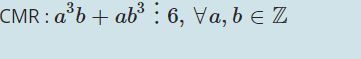
Sáng nay đề chuyên Nguyễn Huệ khó lắm ạ mình làm được mỗi câu a. :(
Anh đã đọc :)