Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-x_2^2-2x_2+2}{x_1-x_2}\)
\(=\left(x_1+x_2\right)-2\)
Vì \(x_1;x_2\in\left(-\infty;1\right)\) thì \(\left\{{}\begin{matrix}x_1< 1\\x_2< 1\end{matrix}\right.\Leftrightarrow\left(x_1+x_2\right)< 2\)
\(\Leftrightarrow\left(x_1+x_2\right)-2< 0\)
Vậy: Hàm số nghịch biến trên \(\left(-\infty;1\right)\)

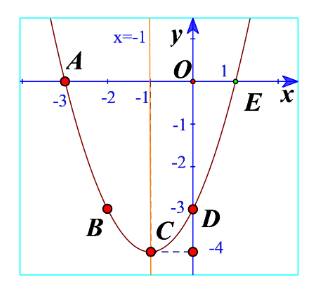
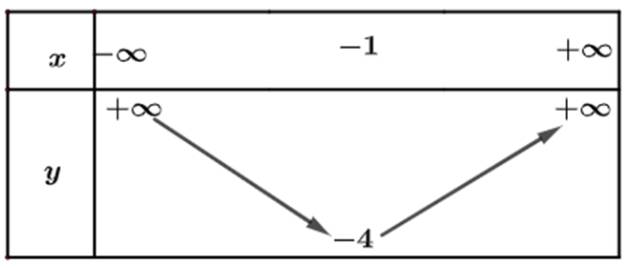
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
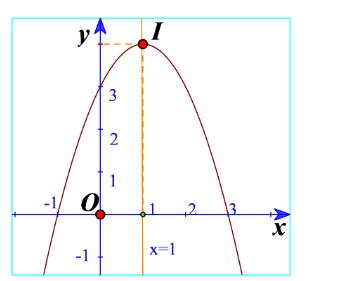
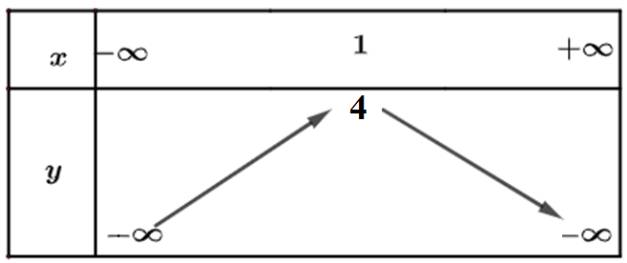
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:

a.
Do (P) đi qua F, thay tọa độ F vào phương trình (P) ta được:
\(a.0^2+b.0+c=5\Rightarrow c=5\)
Do (P) có đỉnh \(I\left(3;-4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=3\\a.3^2+b.3+c=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3b+5=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3.\left(-6a\right)=-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)
hay pt (P) có dạng: \(y=x^2-6x+5\)
b. Em tự giải