Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{4}=\frac{y}{5}=\frac{2x}{8}=\frac{3y}{15}=\frac{2x+3y}{8+15}=\frac{46}{23}=2\)
+) \(\frac{x}{4}=2\Rightarrow x=8\)
+) \(\frac{y}{5}=2\Rightarrow y=10\)
Vậy \(x=8,y=10\)

a.
\(\left|x-3,5\right|\ge0\)
\(\Rightarrow0,5-\left|x-3,5\right|\le0,5\)
Vậy giá trị lớn nhất của biểu thức trên là 0,5 khi |x - 3,5| = 0 <=> x = 3,5
b.
\(\left|1,4-x\right|\ge0\)
\(-\left|1,4-x\right|\le0\)
\(-\left|1,4-x\right|-2\le-2\)
Vậy giá trị nhỏ nhất của biểu thức trên là -2 khi |1,4 - x| = 0 <=> x = 1,4
Chúc bạn học tốt ^^

\(\frac{x}{2}=\frac{y}{-5}\) và \(x-y=-7\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{-5}=\frac{x-y}{2+5}=\frac{-7}{7}=-1\)
=> \(\begin{cases}x=-2\\x=5\end{cases}\)

\(\sqrt{2^x}=2\\ \left(\sqrt{2^x}\right)^2=2^2\\ 2^x=4\\ 2^x=2^2\\ x=2\\ \Rightarrow x^2=2^2\\ \Rightarrow x^2=4\)
\(\sqrt{x^2}=2\\\left(\sqrt{x^2}\right)^2=2^2\\ x^2=4\\ x^2=2^2\\\Rightarrow x=2\)

a) 6 . 63 = 9 . 42
\(\frac{6}{9}=\frac{42}{63}\) ; \(\frac{6}{42}=\frac{9}{63}\) ; \(\frac{9}{6}=\frac{42}{63}\) ; \(\frac{42}{6}=\frac{63}{9}\)
b) 0,24 . 1,61 = 0,84 . 0,46
\(\frac{0,24}{0,84}=\frac{0,46}{1,61}\) ; \(\frac{0,24}{0,46}=\frac{0,84}{1,61}\) ; \(\frac{0,84}{0,24}=\frac{1,61}{0,46}\) ; \(\frac{0,46}{0,24}=\frac{1,61}{0,84}\)
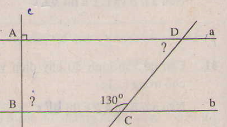

a) Ta có : a vuông góc c (kí hiệu)
b vuông góc c (_____)
Do đó a//b
b) Ta có: C1 = C2 = 130o(đối đỉnh)
Do a//b nên C+ D = 180o(trong cp)
=> D = 50
(Tương tự, B cx v)