PQ
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
VD
23 tháng 4 2020
Bài 3.
Tính số học sinh của lớp 6A.
lớp của 6A trường câụ là bao nhiêu rồi ghi vó là được
chúc bạn học tốt
❤
6 tháng 2 2018
cái này dễ nà!
ta có:
5x + 2 ⋮ x + 1
=> (5x+5) - 5 + 2 ⋮ x + 1
=> (5x+5.1) - 3 ⋮ x + 1
=> 5(x+1) - 3 ⋮ x + 1
có x+1 ⋮ x+1 => 5 (x+1) ⋮ x + 1
=> - 3 ⋮ x + 1
=> x + 1 ∈ Ư(-3)
x ∈ Z => x + 1 ∈ Z
=> x + 1 ∈ {-1;-3;1;3}
=> x ∈ {-2;-4;0;2}
vậy____
KT
6 tháng 2 2018
\(5x+2\)\(⋮\)\(x+1\)
\(\Leftrightarrow\)\(5\left(x+1\right)-3\)\(⋮\)\(x+1\)
Ta thấy \(5\left(x+1\right)\)\(⋮\)\(x+1\)
\(\Leftrightarrow\)\(3\)\(⋮\)\(x+1\)
\(\Rightarrow\)\(x+1\)\(\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\)\(x=\left\{-4;-2;0;2\right\}\)
🤔
HH
10 tháng 8 2017
Ta có: \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\) \(=\dfrac{1+4+7+...+298}{299}\)
Tính riêng mãu ta được: \(1+4+7+...+298=\dfrac{\left[\left(298-1\right):3+1\right].\left(298+1\right)}{2}\)
\(=14950\)
Ghép vào vs mẫu ta được: \(\dfrac{14950}{299}\) \(=50\)
Vậy \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}=50\).
MV
10 tháng 8 2017
rối mắt quá nhá
\(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\\ =\dfrac{1+4+7+...+298}{299}\\ =\dfrac{\left(\dfrac{298-1}{3}+1\right)\cdot\left(298+1\right)}{2}:299\\ =\dfrac{100\cdot299}{2}\cdot\dfrac{1}{299}\\ =\dfrac{100\cdot299}{2\cdot299}\\ =50\)
8 tháng 3 2020
Bài 5:
a) Ta có: \(\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)
\(\Rightarrow\widehat{zOx}=\widehat{xOy}-\widehat{yOz}=180^0-80^0=100^0\)
b) Hai góc có phụ nhau vì:
OM là tia phân giác \(\widehat{xOz}\Rightarrow\widehat{mOz}=\frac{1}{2}\widehat{xOz}\)
ON là tia phân giác \(\widehat{yOz}\Rightarrow\widehat{nOz}=\frac{1}{2}\widehat{yOz}\)
=> \(\widehat{mOz}+\widehat{nOz}=\widehat{mOn}=\frac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=\frac{1}{2}\widehat{xOy}=\frac{1}{2}180^0=90^0\)
8 tháng 3 2020
Bài 4:
a) Số học sinh giỏi của lớp là:
\(40\cdot\frac{1}{5}=8\left(em\right)\)
Số học sinh trung bình của lớp là:
\(\left(40-8\right)\cdot\frac{3}{8}=12\left(em\right)\)
Số học sinh khá của lớp là:
40-8-12=20 (em)
b) Tỉ số phần trăm của học sinh trung bình đối với cả lớp là:
12:40 x 100=30%
Bài 5:
x O y z n m
a) Có \(\widehat{xOy}\)là góc bẹt => \(\widehat{xOy}=180^o\)
Vì tia từ O vẽ tia Oz sao cho góc yOz=80\(^o\)
=> \(\widehat{xOz}=\widehat{xOy}-\widehat{yOz}\)
Thay \(\widehat{xOy}=180^o\left(cmt\right);\widehat{yOz}=80^o\left(gt\right)\)
=> \(\widehat{xOz}=180^0-80^o=100^o\)
Vậy góc xOz=100\(^o\)
b) Vì Om và On lần lượt là phân giác của góc xOz và góc yOz (gt)
\(\Rightarrow\hept{\begin{cases}\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}=\frac{100^0}{2}=50^o\\\widehat{zOn}=\widehat{nOy}=\frac{\widehat{zOy}}{2}=\frac{80^o}{2}=40^o\end{cases}}\)
\(\Rightarrow\widehat{mOz}+\widehat{zOn}=50^o+40^o=90^o\)
=> Góc mOz và zOn có phụ nhau
2 tháng 5 2017
\(A=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{50^2}\)
\(A< 1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{49.50}\)
\(=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
\(=1+1-\frac{1}{50}\)
\(=2-\frac{1}{50}< 2\)
\(\Rightarrow A< 2\)
Q
2 tháng 5 2017
Ta có : \(\frac{1}{1^2}=1\)
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
................................
\(\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow A< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}\)
\(\Rightarrow A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1+1-\frac{1}{50}=2-\frac{1}{50}\left(Đpcm\right)\) . Vậy A < 2
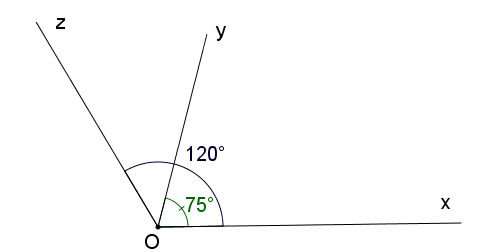
Vì trên cùng 1 nữa mặt phẳng bờ chưa tia Ox có :
xOy < xOz ( do 75o < 120o )
=> Tia Oy nằm giưuax hai tia Ox và Oz
=> xOy + yOz = xOz mà xOy = 75o ; xOz = 120o
=> 75o + yOz = 120o
=> yOz = 120o - 75o = 45o
Từ hình vẽ , ta có :
yOz = xOz-xOy
= 120o-75o
=45o