Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Gọi phân số đó là \(\frac{a}{b}\)
ĐK: (a,b khác 0 và cùng dấu)
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Rightarrow\left(a-b\right)^2\ge0\)
Vậy: đpcm
Gọi phân số dương là a/b. Không mất tính tổng quát, giả sử a>0, b>0 và a≥b. Ta có thể viết a=b+m (m≥0). Ta có:
(a/b)+(b/a)=b/(b+m)≥1+[m/(b+m)]+[b/(b+m)]=1+[(m+b)/(b+m)]=2.
Vậy (a/b)+(b/a)=2
Dấu đẳng thức xảy ra khi a=b (m=0).

Các kết quả trên đều đúng nên mình điền luôn kết quả nha bạn:
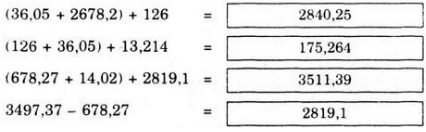
(36,05+2678,2)+126=2840,25.
(126+36,05)+13,214=175,264.
(678,27+14,02)+2819,1=3511,39.
3497,37-678,27=2819,1.
Đó là kết quả của mình có gì sai thì mog pn chỉ ra và giúp mik sửa lỗi nhé!
- Các phép cộng đều cho kết quả đúng.
- Ta có:
(36,05 + 2678,2) + 126
= 36,05 + (2678,2 + 126) (Tính chất kết hợp)
= 36,05 + 2804,2 (theo a)
= 2840,25 (theo c)
(126 + 36,05) + 13,214
= 126 + (36,05 + 13,214) (tính chất kết hợp)
= 126 + 49,264 (theo b)
= 175,264 (theo d)
(678,27 + 14,02) + 2819,1
= (678,27 + 2819,1) + 14,02 (Tính chất giao hoán và kết hợp)
= 3497,37 + 14,02 (theo e)
= 3511,39 (theo g)
3497,37 – 678,27 = 2819,1 (suy từ e)
Vì vậy ta có thể điền số thích hợp và ô trống mà không cần tính toán:


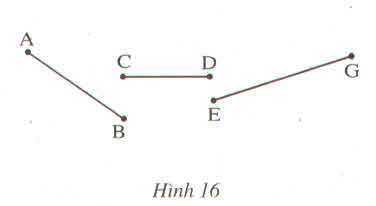
Muốn biết tổng độ dài các đoạn thẳng ở hình 16 trong 1 lần đo , ta dùng compa ''chuyển '' các đoạn thẳng AB ; CD; EG lên một đường thẳng sao cho mút C trùng mút B , mút E trùng mút D . Đo đoạn thẳng EG ta có :
AG = AB + CD + EG = 6 cm
Vậy tổng độ dài ba đoạn thẳng đó là 6 cm
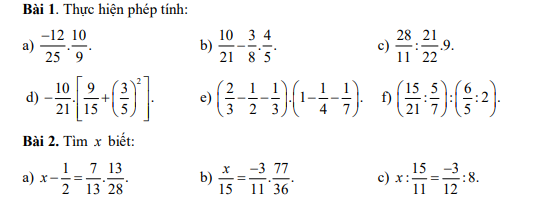


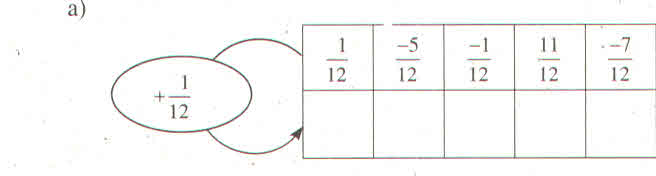
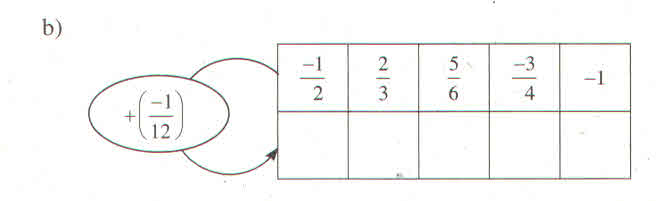







Bài 2:
a: \(x-\dfrac{1}{2}=\dfrac{7}{13}\cdot\dfrac{13}{28}\)
=>\(x-\dfrac{1}{2}=\dfrac{7}{28}=\dfrac{1}{4}\)
=>\(x=\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{3}{4}\)
b: \(\dfrac{x}{15}=\dfrac{-3}{11}\cdot\dfrac{77}{36}\)
=>\(\dfrac{x}{15}=\dfrac{-3}{36}\cdot\dfrac{77}{11}=7\cdot\dfrac{-1}{12}=-\dfrac{7}{12}\)
=>\(x=-\dfrac{7}{12}\cdot15=-\dfrac{105}{12}=-\dfrac{35}{4}\)
c: \(x:\dfrac{15}{11}=\dfrac{-3}{12}:8\)
=>\(x:\dfrac{15}{11}=-\dfrac{1}{4}:8=-\dfrac{1}{32}\)
=>\(x=-\dfrac{1}{32}\cdot\dfrac{15}{11}=\dfrac{-15}{352}\)
Bài 1:
a: \(\dfrac{-12}{25}\cdot\dfrac{10}{9}=\dfrac{-12}{9}\cdot\dfrac{10}{25}=\dfrac{-4}{3}\cdot\dfrac{2}{5}=\dfrac{-8}{15}\)
b: \(\dfrac{10}{21}-\dfrac{3}{8}\cdot\dfrac{4}{5}\)
\(=\dfrac{10}{21}-\dfrac{12}{40}\)
\(=\dfrac{10}{21}-\dfrac{3}{10}=\dfrac{100-63}{210}=\dfrac{37}{210}\)
c: \(\dfrac{28}{11}:\dfrac{21}{22}\cdot9=\dfrac{28}{11}\cdot\dfrac{22}{21}\cdot9\)
\(=\dfrac{28}{21}\cdot\dfrac{22}{11}\cdot9=\dfrac{4}{3}\cdot2\cdot9=\dfrac{4}{3}\cdot18=24\)
d: \(-\dfrac{10}{21}\cdot\left[\dfrac{9}{15}+\left(\dfrac{3}{5}\right)^2\right]\)
\(=\dfrac{-10}{21}\cdot\left[\dfrac{3}{5}+\dfrac{9}{25}\right]\)
\(=\dfrac{-10}{21}\cdot\dfrac{15+9}{25}\)
\(=\dfrac{-10}{25}\cdot\dfrac{24}{21}=\dfrac{-2}{5}\cdot\dfrac{8}{7}=\dfrac{-16}{35}\)
e: \(\left(\dfrac{2}{3}-\dfrac{1}{2}-\dfrac{1}{3}\right)\cdot\left(1-\dfrac{1}{4}-\dfrac{1}{7}\right)\)
\(=\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\cdot\dfrac{28-7-4}{28}\)
\(=\dfrac{-1}{6}\cdot\dfrac{17}{28}=\dfrac{-17}{168}\)
f: \(\left(\dfrac{15}{21}:\dfrac{5}{7}\right):\left(\dfrac{6}{5}:2\right)\)
\(=\left(\dfrac{5}{7}\cdot\dfrac{7}{5}\right):\left(\dfrac{6}{5\cdot2}\right)\)
\(=1:\dfrac{6}{10}=\dfrac{10}{6}=\dfrac{5}{3}\)