Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)

\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
Ta có: \(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(2A=1-\dfrac{1}{5}+\dfrac{1}{5}+...+\dfrac{1}{29}-\dfrac{1}{41}\)
\(2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(A=\dfrac{20}{41}\)
Lại có: \(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(3B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+...+\dfrac{1}{19}-\dfrac{1}{31}\)
\(3B=1-\dfrac{1}{31}=\dfrac{30}{31}\)
\(B=\dfrac{10}{31}\)
Vì \(\dfrac{20}{41}>\dfrac{10}{31}\) nên...

\(3n-2\inƯ\left(15\right)\) \(=\left\{1;-1;3;-3;5;-5;15;-15\right\}.\)
\(\Leftrightarrow n\in\left\{1;\dfrac{1}{3};\dfrac{5}{3};\dfrac{-1}{3};\dfrac{7}{3};-1;\dfrac{17}{3};\dfrac{-13}{3}\right\}.\)
Mà \(n\ne\dfrac{2}{3};n\in Z.\)
\(\Rightarrow n\in\left\{1;-1\right\}.\)

a) Ư(60):{ 1;2;3;4;5;6;10;12;15;20;30;60}
Ư(84):{ 1;2;4;6;7;12;14;21;42;84}
Ư(120):{ 1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}
ƯC(60;84;120):{ 2;4;6;12}
nhưng vì x_> 6 nên x = 2,4,6

\(\frac{2^3.3}{2^2.3^2.5}=\frac{2}{3.5}=\frac{2}{15}\)
Thiếu dấu nhân ở chỗ \(2^2.3^2\)nha

2006 . 125 + \(\dfrac{1000}{126}\) . 2005 - 888 = 265774,6984


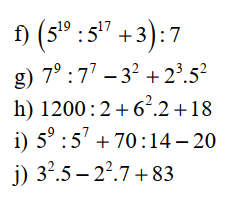 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim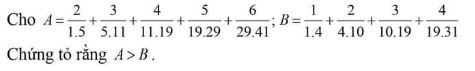

 các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
đk : \(n\ne-\dfrac{1}{3}\)
gọi d là ƯCLN(18n+3,21n+7)
ta có 18n+3chia hết cho d
21n+7 chia hết cho d
⇔21n+7-18n-3 chia hết cho d
⇔126n+42-126n-21 chia hết cho d
21 chia hết cho d
⇒d∈Ư(21)=1;3;7;21
n ≠ 3k-1;3k-3;3k-7;3k-21