K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MS
0
Thông cảm mk bị cận!
23 tháng 7 2017
sửa lại đề nè:
So sánh: 291 và 535
Ta có: 291 = (213)7 = 81927
535 = (55)7 = 31257
Vì 81927>31257
=> 291>535
23 tháng 4 2017
Giải:
Do \(\left(2016a+13b-1\right)\left(2016^a+2016a+b\right)\) \(=2015\)
Nên \(2016a+13b-1\) và \(2016^a+2016a+b\) là 2 số lẻ \((*)\)
Ta xét 2 trường hợp:
Trường hợp 1: Nếu \(a\ne0\) thì \(2016^a+2016a\) là số chẵn
Do \(2016^a+2016a+b\) lẻ \(\Rightarrow b\) lẻ
Với \(b\) lẻ \(\Rightarrow13b-1\) chẵn do đó \(2016a+13b-1\) chẵn (trái với \((*)\))
Trường hợp 2: Nếu \(a=0\) thì:
\(\left(2016.0+13b-1\right)\left(2016^0+2016.0+b\right)\) \(=2015\)
\(\Leftrightarrow\left(13b-1\right)\left(b+1\right)=2015=1.5.13.31\)
Do \(b\in N\Rightarrow\left(13b-1\right)\left(b+1\right)=5.403=13.155\) \(=31.65\)
Và \(13b-1>b+1\)
\(*)\) Nếu \(b+1=5\Rightarrow b=4\Rightarrow13b-1=51\) (loại)
\(*)\) Nếu \(b+1=13\Rightarrow b=12\Rightarrow13b-1=155\) (chọn)
\(*)\) Nếu \(b+1=31\Rightarrow b=30\Rightarrow13b-1=389\) (loại)
Vậy \(\left(a,b\right)=\left(0;12\right)\)
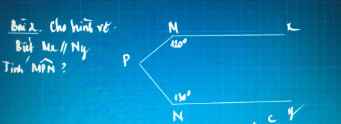
Kẻ Pz//Mx//Ny
\(\Rightarrow\left\{{}\begin{matrix}\widehat{MPz}+\widehat{PMx}=180^0\\\widehat{NPz}+\widehat{PNy}=180^0\end{matrix}\right.\)(trong cùng phía)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{MPz}=180^0-\widehat{PMx}=180^0-120^0=60^0\\\widehat{NPz}=180^0-\widehat{PNy}=180^0-130^0=50^0\end{matrix}\right.\)
\(\Rightarrow\widehat{MPN}=\widehat{MPz}+\widehat{NPz}=60^0+50^0=110^0\)
Kẻ Pz//Mx//Ny
\(\Rightarrow\left\{{}\begin{matrix}\widehat{xMP}+\widehat{MPz}=180^0\\\widehat{yNP}+\widehat{NPz}=180^0\end{matrix}\right.\left(trong.cùng.phía\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{MPz}=180^0-120^0=60^0\\\widehat{NPz}=180^0-150^0=30^0\end{matrix}\right.\\ \Rightarrow\widehat{MPN}=\widehat{MPz}+\widehat{NPz}=90^0\)