
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)

Gọi độ dài cạnh của mỗi ô vuông là 1.
Theo định lí Py-ta-go:
AB2 = 12 + 22 = 1 + 4 = 5
BC2 = 12 + 22 = 1 + 4 = 5
AC2 = 12 + 32 = 1 + 9 = 10
Do AB2 = BC2 nên AB = BC
Do AB2 + BC2 = AC2 nên \(\widehat{ABC}=90^o\)
Vậy \(\Delta ABC\) vuông cân tại B.

-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
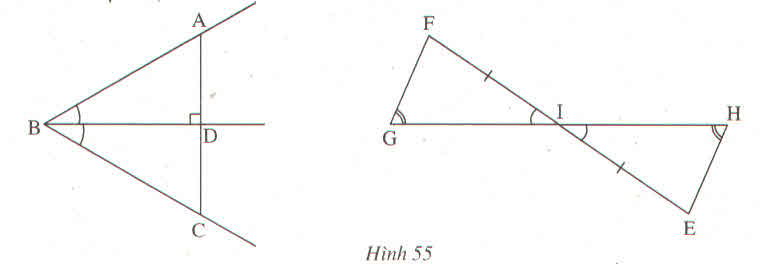
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH

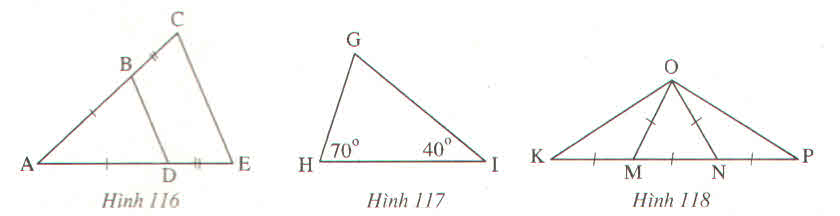
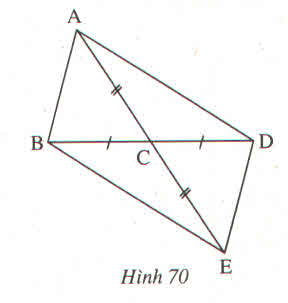
Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha

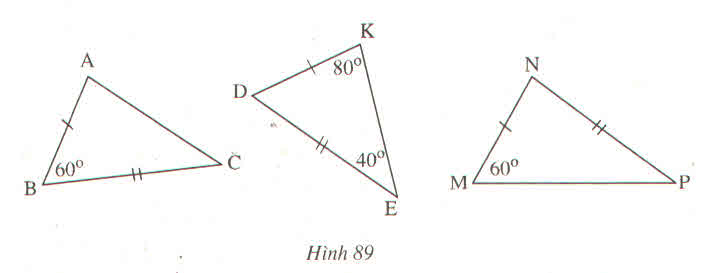
Tam giác DKE có:
\(\widehat{D}+\widehat{K}+\widehat{E}\)=1800 (tổng ba góc trong của tam giác).
\(\widehat{D}\)+800 +400=1800
\(\widehat{D}\)=1800 -1200= \(60^0\)
Nên ∆ ABC và ∆KDE có:
AB=KD(gt)
\(\widehat{B}\)=\(\widehat{D}\)=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại.

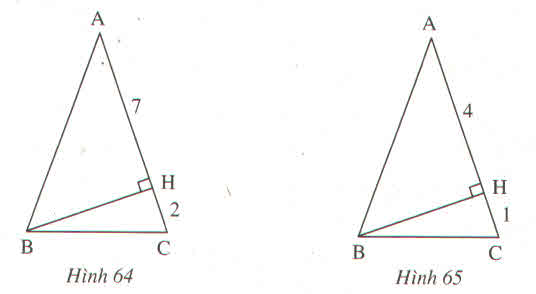
câu a: có 2 bước
bước 1 : tính cạnh BH
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)


Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)

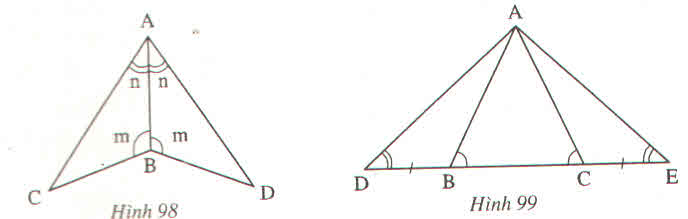
- Xem hình 98
∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
- Xem hình 99.
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)
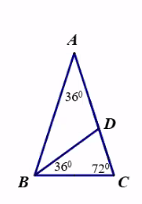 Tìm các tam giác cân trên hình vẽ sau
Tìm các tam giác cân trên hình vẽ sau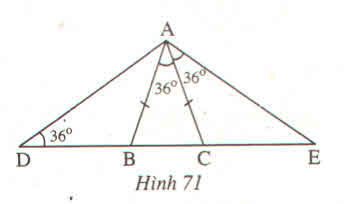

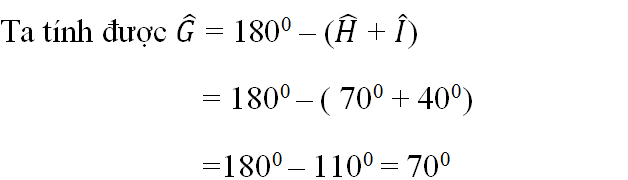







Xét ΔBDC có:
\(\widehat{BDC}+\widehat{BCD}+\widehat{DBC}=180^o\\ \Rightarrow36^o+72^o+\widehat{BDC}=180^o\\ \Rightarrow\widehat{BDC}=72^o\)
Vì \(\widehat{BDC}=\widehat{BCD}\) nên ΔBDC cân tại B
Xét ΔABC có:
\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\\ \Rightarrow36^o+72^o+\widehat{ABC}=180^o\\ \Rightarrow\widehat{ABC}=72^o\)
Vì \(\widehat{ABC}=\widehat{ACB}\) nên ΔABC cân tại A
36