Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xếp Phúc Đức cạnh nhau có \(2!\) cách
Xếp 4 học sinh nữ có \(4!\) cách
4 học sinh nữ tạo ra 5 khe trống, xếp cặp Phúc-Đức và 3 học sinh nam còn lại vào 5 khe trống này có: \(A_5^4\) cách
\(\Rightarrow2!.4!.A_5^4\) cách xếp thỏa mãn

Giải thích các bước giải:
Xếp 4 bạn nam (trừ A1) và 2 bạn nữ(trừ B1) thành 1 dãy ta có 6! cách xếp
Sau đó xếp A1 và B1 vào giữa các bạn đã xếp do A1, B1 không ngồi cạnh nhau nên ta có 2 trường hợp sau:
TH1: A1 xếp ở đầu nên do khi các bạn ngồi thành bàn tròn thì suy ra B1 không được xếp ở cuối như vậy B1 có 5 cách chọn => Tương tự với B1 ở đầu => có 6!.5.2 = 7200 cách xếp
TH2: A1, B1 đều không xếp ở đầu hàng => có 5C2 cách chọn vị trí cho 2 bạn
=> có 6!.5C2.2 = 14400 cách xếp
=> có tất cả 21600 cách xếp

Xếp 4 bạn nam (trừ A1) và 2 bạn nữ(trừ B1) thành 1 dãy ta có 6! cách xếp
Sau đó xếp A1 và B1 vào giữa các bạn đã xếp do A1, B1 không ngồi cạnh nhau nên ta có 2 trường hợp sau:
TH1: A1 xếp ở đầu nên do khi các bạn ngồi thành bàn tròn thì suy ra B1 không được xếp ở cuối như vậy B1 có 5 cách chọn => Tương tự với B1 ở đầu => có 6!.5.2 = 7200 cách xếp
TH2: A1, B1 đều không xếp ở đầu hàng => có 5C2 cách chọn vị trí cho 2 bạn
=> có 6!.5C2.2 = 14400 cách xếp
=> có tất cả 21600 cách xếp
~ Chúc bn hok tốt ~
Giải thích các bước giải:
Xếp 4 bạn nam (trừ A1) và 2 bạn nữ(trừ B1) thành 1 dãy ta có 6! cách xếp
Sau đó xếp A1 và B1 vào giữa các bạn đã xếp do A1, B1 không ngồi cạnh nhau nên ta có 2 trường hợp sau:
TH1: A1 xếp ở đầu nên do khi các bạn ngồi thành bàn tròn thì suy ra B1 không được xếp ở cuối như vậy B1 có 5 cách chọn => Tương tự với B1 ở đầu => có 6!.5.2 = 7200 cách xếp
TH2: A1, B1 đều không xếp ở đầu hàng => có 5C2 cách chọn vị trí cho 2 bạn
=> có 6!.5C2.2 = 14400 cách xếp
=> có tất cả 21600 cách xếp

Chọn D
Xếp ngẫu nhiên tám học sinh thành hàng ngang, có 8! cách. Suy ra n ( Ω ) = 8! = 40320
Gọi A là biến cố cần tính xác suất.
Ta coi Hoàng, Lan, Nam ( Lan ở giữa) là một nhóm. Khi đó vì hai bên nhóm này bắt buộc là nữ nên coi nhóm này là một nam. Vậy có thể coi ta có ba nam và ba nữ.
Khi đó có hai trường hợp xảy ra.
Trường hợp 1: Nam ngồi vị trí lẻ.
Xếp ba nam vào vị trí lẻ có 3! cách.
Xếp ba nữ vào vị trí chẵn có 3! cách.
Hoán vị hai học sinh nam trong nhóm ( Hoàng- Lan- Nam) có 2! cách.
Vậy số cách sắp xếp trong trường hợp này là 3!.3!.2! = 72 cách.
Trường hợp 2: Nam ngồi vị trí chẵn.
Tương tự trường hợp này có 3!.3!.2! = 72 cách.
Suy ra n(A) = 72 + 72 = 144 cách.
Vậy 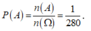

Đáp án B
– Số phần tử của không gian mẫu n Ω =10!
* Xếp 10 học sinh trên một hàng ngang sao cho 5 học sinh nam xen kẽ 5 học sinh nữ có 2 cách xếp.
* Xét trong 2 cách xếp trên các khả năng Hoàng và Lan đứng liền kề nhau:
+ Xếp 8 học sinh trên một hàng ngang sao cho 4 học sinh nam xen kẽ 4 học sinh nữ có 2 cách xếp.
+ Với mỗi cách xếp 8 học sinh trên có 9 khoảng trống tạo ra. Với mỗi khoảng trống trên, xếp Hoàng và Lan vào khoảng trống này để được 5 học sinh nam xen kẽ 5 học sinh nữ có 1 cách xếp.
xxxx
Suy số cách xếp 5 học sinh nam xen kẽ 5 học sinh nữ mà Hoàng và Lan đứng kề nhau là: 2.9
Vậy số phần tử của A là: n =2-2.9=18432.


Chọn C
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có A 7 5 = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 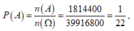


aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa