
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

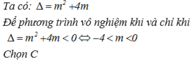

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Lời giải:
PT $\Leftrightarrow (x+1)^2+|x+1|-(m+1)=0$
$\Leftrightarrow |x+1|^2+|x+1|-(m+1)=0$
Đặt $|x+1|=t(t\geq 0)$ thì: $t^2+t-(m+1)=0(*)$
Với $m=1$ thì $t^2+t-2=0$
$\Leftrightarrow (t-1)(t+2)=0$
Vì $t\geq 0$ nên $t=1\Leftrightarrow |x+1|=1$
$\Leftrightarrow x+1=\pm 1\Leftrightarrow x=0$ hoặc $x=-2$
Để pt vô nghiệm thì $(*)$ chỉ có nghiệm âm hoặc vô nghiệm.
PT $(*)$ chỉ có nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=1+4(m+1)\geq 0\\ S=-1< 0\\ P=-(m+1)<0\end{matrix}\right.\Leftrightarrow m>-1\)
Để $(*)$ vô nghiệm khi $\Delta=4m+5< 0$
$\Leftrightarrow m< \frac{-5}{4}$
Vậy $m>-1$ hoặc $m< \frac{-5}{4}$

a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn

mx²+2(m-1)x+4 ≥0
bpt trên vô nghiệm <=>mx²+2(m-1)x+4 <0
a=m\(\ne0\)
\(\Delta'=\left(m-1\right)^2-m.4\)
\(=m^2-2m+1-4m\)
\(=m^2-6m+1\)
\(=\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)\)
bpt vô nghiệm <=>\(\left\{{}\begin{matrix}a< 0\\\Delta'< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\3-2\sqrt{2}< m< 3+2\sqrt{2}\end{matrix}\right.\)
=> không có m để bất phương trình vô nghiệm

Với m = 1 phương trình đã cho có dạng
2 x 2 + 2 = 0 .
Phương trình này vô nghiệm, nên phương án A bị loại. Với m = -1 phương trình đã cho trở thành phương trình bậc nhất 6x + 2 = 0 chỉ có một nghiệm nên phương án B bị loại.
Với m = 2 phương trình đã cho trở thành phương trình
3 x 2 – 3 x + 2 = 0 .
Phương trình này vô nghiệm, nên phương án D bị loại.
Đáp án: C