Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có trong toán vui mỗi tuần đó
Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.

Vận tốc của 2 chị em bằng nhau và xuất phát cùng lúc => 2 chị em gặp nhau ở giữa đường
Quãng đường của em đi được là:
40 : 2 = 20 ( m )
Thời gian để người em đi hết quãng đường là :
20 : 2 = 10 ( giây )
Quãng đường chú chó đi được là :
10 x 3 = 30 ( m )
Đáp số : 300m
Vận tốc của 2 chị em bằng nhau và xuất phát cùng lúc => 2 chị em gặp nhau ở giữa đường
Quãng đường của em đi được là:
40 : 2 = 20 ( m )
Thời gian để người em đi hết quãng đường là :
20 : 2 = 10 ( giây )
Quãng đường chú chó đi được là :
10 x 3 = 30 ( m )
Đáp số : 300m

Bài 1:
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x
⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625,
√∆’ = 25
x1 = 5 – 25 = -20,
x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Vậy Vận tốc của xuồng khi đi là 30 km/h
Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt nên :
4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt

Bài 1:Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
--Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
--khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
--Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt
nên : 4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt
tk nha

1 giờ 15 phút = 1.25 giờ
38km 400m = 38400 m
Trung bình mỗi giờ người đó đi được:
38400 : 1,25 = 30720 (m)
Đ/s....

Gọi vận tốc của người xuất phát từ A là x, của người đi từ B là y (km/phút).
Điều kiện là x, y > 0.
Khi gặp nhau tại địa điểm C cách A là 2km :

Thời gian người xuất phát từ A đi đến C là: 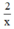 (phút)
(phút)
Thời gian người xuất phát từ B đi đến C là: 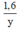 (phút).
(phút).
Vì hai người cùng xuất phát nên ta có phương trình:
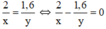
Mà nhận thấy trong cùng một thời gian, quãng đường người đi từ A đi được lớn hơn quãng đường người đi từ B đi được, do đó suy ra x > y.
Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn (người đi từ B) xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường.
Khi đó, mỗi người đi được 1,8 km, Thời gian hai người đi lần lượt là: 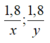
Vậy ta có phương trình:
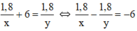
Ta có hệ phương trình 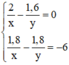
Đặt 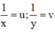 , khi đó hệ phương trình trở thành:
, khi đó hệ phương trình trở thành:
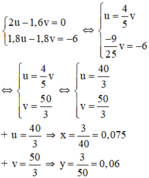
Vậy vận tốc của người đi từ A là 0,075 km/phút = 4,5 km/h;
vận tốc của người đi từ B là 0,06 km/phút = 3,6 km/h.
Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.
Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.