Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
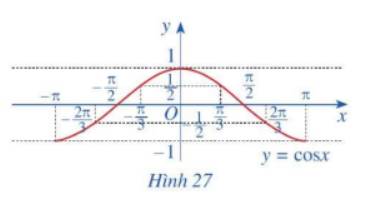
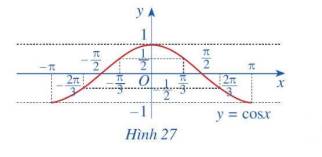
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
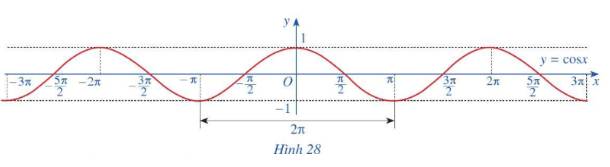
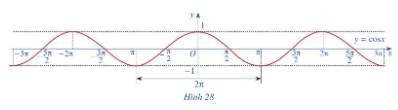
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

Vật đi qua vị trí cân bằng thì x = 0
Khi đó
\(\begin{array}{l}2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\\Leftrightarrow t = \frac{2\pi }{15} + \frac{{k\pi }}{5} ;k \in Z\end{array}\)
Do khoảng thời gian từ 0 đến 6 giây nên \(t \in \left[ {0;6} \right]\)
\(\begin{array}{l}0 \le \ \frac{{2\pi }}{{15}} + \frac{{k\pi }}{5} \le \ 6;k \in Z\\ \Rightarrow \frac{-2 }{3}\le \ k \le \ \frac{90 - 2\pi}{3\pi};k \in Z\end{array}\)
Do \(k \in Z\) nên \(k \in \left\{ {0;1;2;3;4;5;6;7;8} \right\}\)
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.

a)
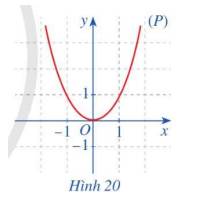
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
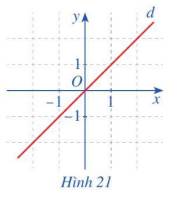
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d

Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.

Tham khảo:
a,

\(\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2\)
b) Lấy dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta có \(f\left( {{x_n}} \right) = 2{x_n}.\)
\(\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2\)

Đáp án B
Số phần tử không gian mẫu bằng 7 3 và số kết quả thuận lợi cho biến cố bằng 7.6.5
và xác suất cần tính bằng 7 . 6 . 5 7 3 = 30 49

Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
| Raashan |
Sylvia |
Ted |
| 1 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
1 |
0 |
| 2 |
0 |
1 |
| 1 |
2 |
0 |
| 0 |
2 |
1 |
| 1 |
0 |
2 |
| 0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là Raashan → Sylvia → Ted Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có 1 4 cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan ⇆ Sylvia và Ted không nhận được tiền.
Raashan → Sylvia → Ted.
- Raashan → Ted → Sylvia.
- Sylvia → Raashan → Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ 1 4
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
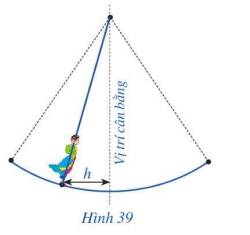



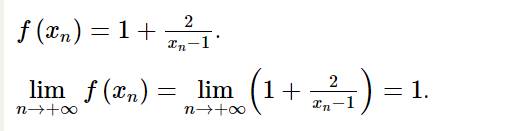
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.
Khi đó
\(\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t - 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t - 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}\)
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.
Khi đó
\(\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}\)