Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

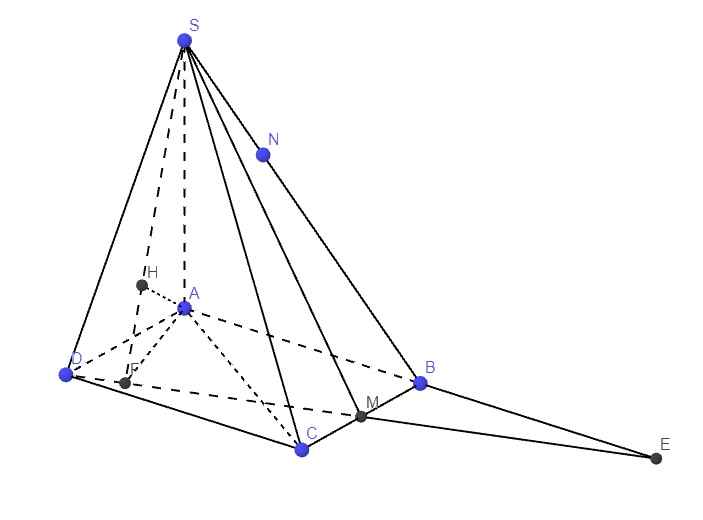
Nối DM và AB kéo dài cắt nhau tại E
Do BM song song và bằng 1 nửa AD \(\Rightarrow BM\) là đường trung bình tam giác ADE
\(\Rightarrow AE=2BE\Rightarrow d\left(B;\left(SMD\right)\right)=\dfrac{1}{2}d\left(A;\left(SMD\right)\right)\)
Lại có: \(\left\{{}\begin{matrix}BN\cap\left(SMD\right)=S\\NS=\dfrac{1}{3}BS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{3}d\left(B;\left(SMD\right)\right)=\dfrac{1}{6}d\left(A;\left(SMD\right)\right)\)
Từ A kẻ AF vuông góc MD (F thuộc MD), từ A kẻ AH vuông góc SF (H thuộc SF)
\(\Rightarrow AH\perp\left(SMD\right)\Rightarrow AH=d\left(A:\left(SMD\right)\right)\)
Hệ thức lượng trong tam giác vuông ADE:
\(\Rightarrow AF=\dfrac{AD.AE}{DE}=\dfrac{AD.2AB}{\sqrt{AD^2+\left(2AB\right)^2}}=\dfrac{8a\sqrt{17}}{17}\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{21}\)
Hệ thức lượng: \(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=...\)
\(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{6}AF=...\)

Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
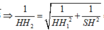
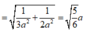
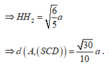
=> Chọn phương án B.

Hình như là bạn ghi ko đúng đề
\(AB'//DC'\) nên \(D\in\left(AB'C'\right)\Rightarrow AD\in\left(AB'C'\right)\)
\(\Rightarrow M\in\left(AB'C'\right)\Rightarrow\) khoảng cách từ M đến (AB'C') bằng 0
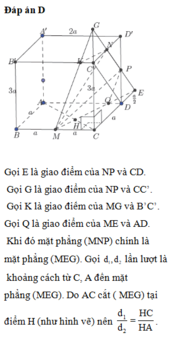

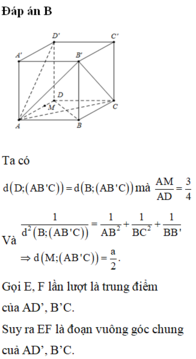
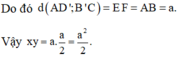
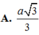
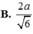
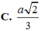
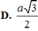
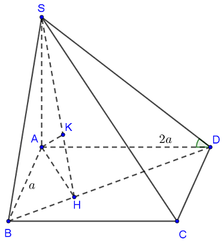
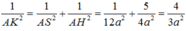
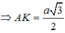

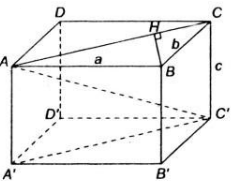

ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
Pytago tính đuợc 3 cạnh ΔAMC
\(AC=a\sqrt{5}\); \(AM=\frac{3a}{2}\), \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức HeronHeron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức HeronHeron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)