Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

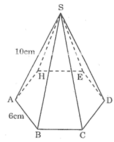
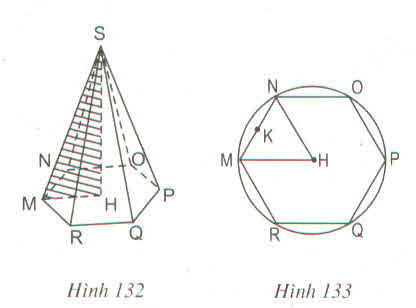
Gọi SO là đường cao của hình chóp
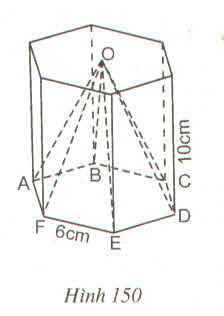
Khi đó △ AOB là tam giác đều cạnh
AB=6cm ⇒ OA=6cm
Trong tam giác vuông SOA áp dụng pi-ta-go ta tính được SO = 8cm
Vậy chọn đáp án B

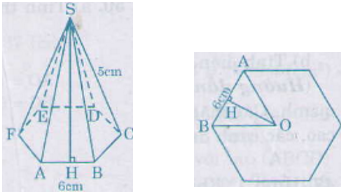
chia đáy hình chóp đều thành 6 phần bằng nhau
diện tích của 1 tam giác đều là : 1/2 . 6 . \(\sqrt{6^2-\left(\dfrac{1}{2}.6\right)^2}\)=3.\(\sqrt{27}\) (cm2
diện tích đáy của hình chóp là : 3.\(\sqrt{27}\).6=18.\(\sqrt{27}\) (cm2)
thể tích của hình chóp là : 1/3 . 18.\(\sqrt{27}\).10=180.\(\sqrt{3}\) (cm3)
vậy đáp án đúng là (C)180\(\sqrt{3}\) cm3

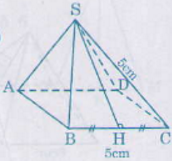
x 6cm 4cm Theo định lý Py - ta - go :
x2 = 42 + 62
⇒ x2 = 16 + 36
⇒ x2 = 52
⇒ x = √52 (cm)
Vậy đáp án (B) là chính xác
Nhắc lại : Đáp án (B)




B