Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng công thức tính trọng lực: \(P=m
.
g\)
Ta có:
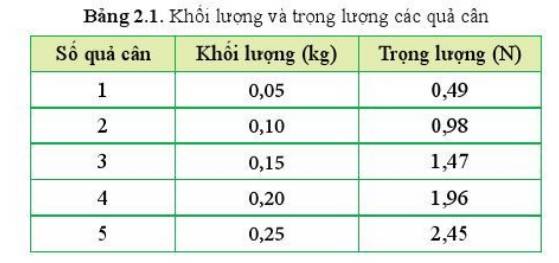
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)

- Các bước tiến hành thí nghiệm:
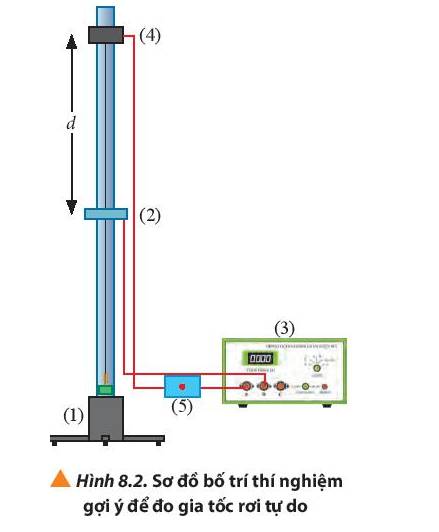
Bước 1: Bố trí thí nghiệm như hình 8.2
+ Lắp nam châm điện ở đầu trên của thanh nhôm, nối với cổng A của đồng hồ điện tử thông qua công tắc điện.
+ Cổng quang điện ở dưới, cách nam châm điện một đoạn d và được nối vào cổng B của đồng hồ.
Bước 2: Điều chỉnh cho giá đỡ thẳng đứng bằng các vít ở đế sao cho quả nặng của dây dọi sẽ nằm ở tâm lỗ tròn. Thiết lập đồng hồ thời gian hiện số chế độ A \( \leftrightarrow \) B để đo thời gian từ lúc thả đến khi vật chắn cổng quang điện.
Bước 3: Đặt vật rơi vào vị trí nam châm điện, dùng êke vuông ba chiều để xác định vị trí ban đầu của vật. Ấn nút RESET trên mặt đồng hồ để đưa chỉ thị số về giá trị 0.000. Nhấn công tắc điện để kích thích vật rơi và khởi động đồng hồ đo thời gian hiện số.
Bước 4: Khi vật rơi và chắn các tia hồng ngoại của cổng quang điện, đồng hồ sẽ dừng. Đọc thời gian rơi trên đồng hồ và ghi số liệu vào bảng.
- Các em tự tiến hành thí nghiệm

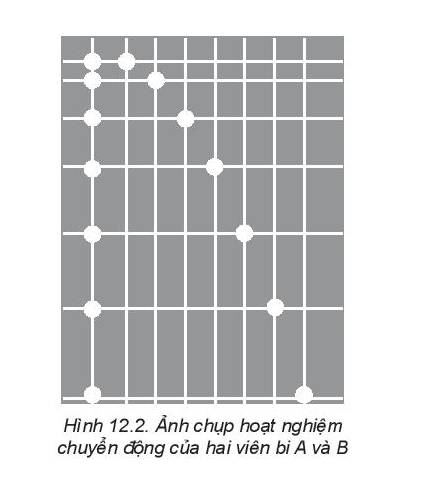
Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian
Mặt khác, ta có \(v=\dfrac{s}{t}=\dfrac{x}{t}\)
(do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi
\(\Rightarrow v_x=v_0\)
1. (a)
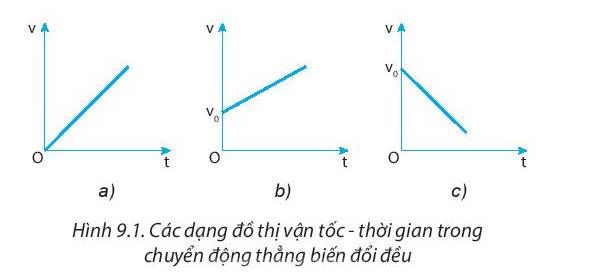
Đồ thị hình a là đường thẳng đi qua gốc tọa độ nên công thức mối liên hệ giữa v, a và t có dạng hàm số \(y=ax\). Công thức cần tìm là: \(v=at\left(a>0\right)\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a>0\right)\) (do đồ thị có dạng dấu sắc (đồng biến)) nên công thức cần tìm là: \(v=v_0+at\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a< 0\right)\) (do đồ thị có dạng dấu huyền (nghịch biến)) nên công thức cần tìm là: \(v=v_0-at\).
(b) Chuyển động nhanh dần đều là các chuyển động ở hình a, b. Chuyển động chậm dần đều là chuyển động ở hình c.
2. Từ thời điểm 0s đến 4s, tức 4s đầu, bạn đi đều với tốc độ 1,5m/s.
Từ thời điểm 4s đến 6s, tức 2s tiếp theo, bạn bắt đầu đi chậm lại từ tốc độ 1,5m/s xuống 0m/s.
Sau đó, từ thời điểm 6s đến 7s, tức 1s tiếp theo, bạn này dừng lại.
Trong 1s tiếp theo, từ thời điểm 7s đến 8s, bạn này bắt đầu đảo chiều đi (đi ngược lại so với chiều đi ban đầu) và bắt đầu chuyển động nhanh dần từ tốc độ 0m/s đến 0,5m/s.
Trong 1s sau đó, từ thời điểm 8s đến 9s, bạn này đi đều với tốc độ 0,5m/s với chiều đi như giây trước.
Cuối cùng, từ thời điểm 9s đến 10s, tức 1s cuối, bạn này đi chậm lại từ tốc độ 0,5m/s và dừng hẳn (tốc độ 0m/s).

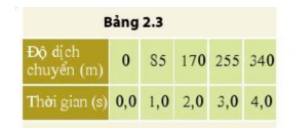
- Vẽ đồ thị độ dịch chuyển – thời gian: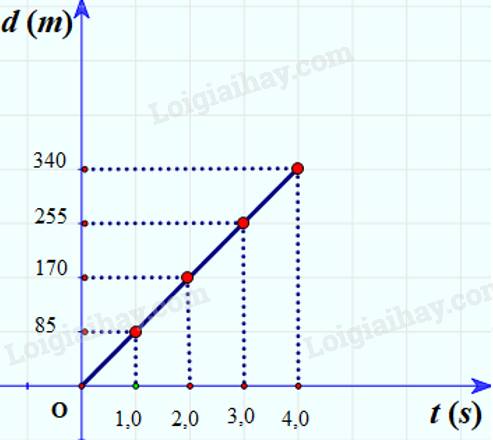
- Vận tốc của xe là:
\(v=\dfrac{d}{t}=85\left(m/s\right)\)

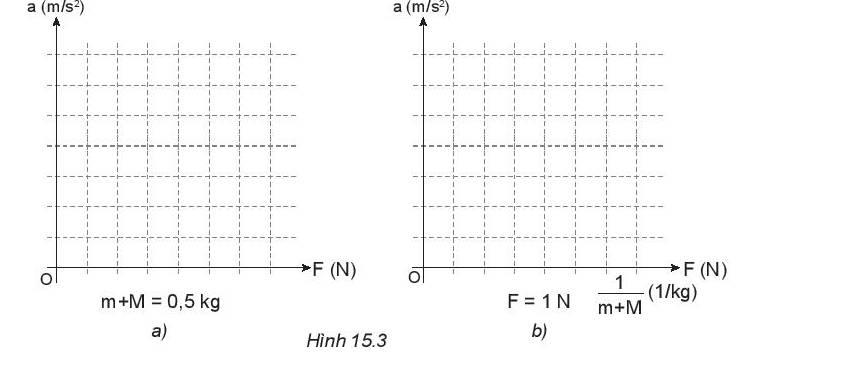
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
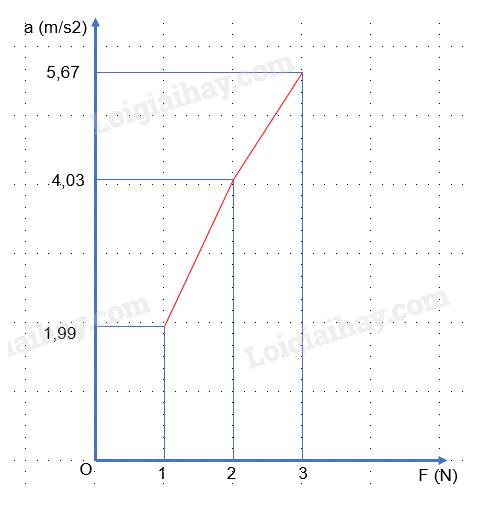
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
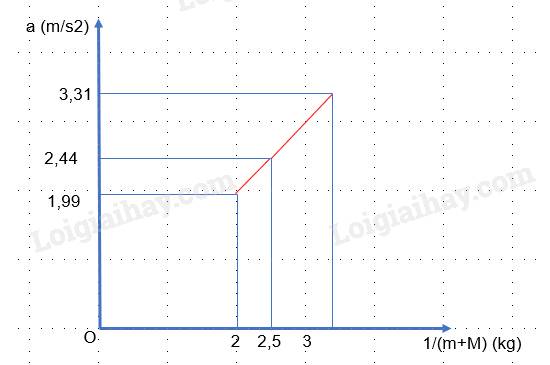
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

1.Sự rơi tự do là sự rơi của các vật chỉ dưới tác dụng của trọng lực.
- Đặc điểm của sự rơi tự do: + Có phương thẳng đứng
+Có chiều từ trên xuống đất
+ Là chuyển động thẳng nhanh dần đều
+Không vận tốc
-Khác nhau :+Sự rơi của các vật trong không khí là do sức cản của không khí
+Sự rơi tự do là do dưới tác dụng của trọng lực
4. a.Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
-Chuyển động thẳng biến đổi đều có quỹ đạo là đường thẳng và độ lớn của vận tốc tức thời tăng(giảm) đều theo thời gian.
-Chuyển động nhanh dần đều là độ lớn của vận tốc tức thời tăng đều theo thời gian.
-Chuyển động chậm dần đều là độ lớn của vận tốc tức thời giảm đều theo thời gian. -Chuyển động tròn là chuyển động có quỹ đạo là một đường tròn. -Chuyển động tròn đều là chuyển động có quỹ đạo tròn và vật đi được những cung tròn bẳng nhau trong những khoảng thời gian bằng nhau bất kì. b.Công thức vận tốc: v=\(\frac{S}{t}\) ;v=\(\frac{\Delta S}{\Delta t}\) ;v=v0 +a\(\times t\) Gia tốc của các loại chuyển động: \(a=\frac{\Delta v}{\Delta t}=\frac{v-v_0}{t-t_0}\) \(a_{ht}=\frac{v^2}{r}=r\times\omega^2\)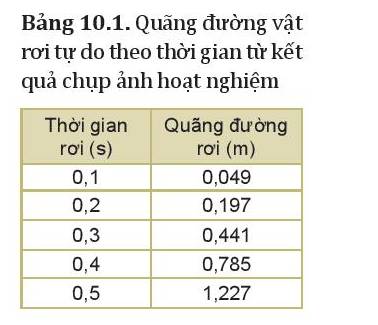





1.
Dựa vào bảng 10.1, ta thấy rằng
+ Trong 0,1 s đầu tiên, vật đi được quãng đường là 0,049 m
+ Trong 0,1 s tiếp theo, vật đi được quãng đường là 0,197 – 0,049 = 0,148 m
+ Từ 0,2 s đến 0,3 s, vật đi được quãng đường là 0,441 – 0,197 = 0,244 m
+ Từ 0,3 s đến 0,4 s, vật đi được quãng đường là 0,785 – 0,441 = 0,344 m
+ Từ 0,4 s đến 0,5 s, vật ssi được quãng đường là 1,227 – 0,785 = 0,442 m
Thông qua các số liệu trên, ta thấy cùng trong một khoảng thời gian, quãng đường vật rơi được càng dài, chứng tỏ vật rơi tự do
2.
Gia tốc của chuyển động rơi tự do
\(a = \frac{{2s}}{{{t^2}}} = \frac{{2.0.049}}{{0,{1^2}}} = 9,8(m/{s^2})\)