PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
CM
25 tháng 8 2018
1. Hàm số mũ
Cho số a > 0 và a ≠ 1. Hàm số y = a x được gọi là hàm số mũ cơ số a.
Các tính chất của hàm số mũ y = a x
| Tập xác định | (-∞; +∞) |
| Đạo hàm | y’= a x .lna |
| Chiều biến thiên | + Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến |
| Tiệm cận | Trục Ox là tiệm cận ngang |
| Đồ thị | Đi qua các điểm (0; 1); (1; a) Nằm phía trên trục hoành ( y = a x > 0 mọi x) |
2. Hàm Logarit
Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a
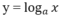
| Tập xác định | (0; +∞) |
| Đạo hàm |  |
| Chiều biến thiên | + Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến |
| Tiệm cận | Trục Oy là tiệm cận đứng |
| Đồ thị | Đi qua các điểm (1; 0); (a; 1) Nằm bên phải trục tung. |
3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.
27 tháng 12 2021
1. Hàm số mũ
Cho số a > 0 và a ≠ 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
Các tính chất của hàm số mũ y = ax
Tập xác định | (-∞; +∞) |
Đạo hàm | y’= ax.lna |
Chiều biến thiên | + Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến |
Tiệm cận | Trục Ox là tiệm cận ngang |
Đồ thị | Đi qua các điểm (0; 1); (1; a) Nằm phía trên trục hoành ( y = ax > 0 mọi x) |
2. Hàm Logarit
Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a
| Tập xác định | (0; +\(\infty\)) |
| Đạo hàm | y' = \(\frac{1}{xIna}\) |
| Chiều biến thiên | + Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến |
| Tiệm cận | Trục Oy là tiệm cận đứng |
| Đồ thị | Đi qua các điểm (1; 0); (a; 1) Nằm bên phải trục tung. |
3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.
HT
CM
25 tháng 5 2018
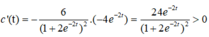
với mọi t ≥ 0 nên c(t) tăng trên [0; +∞] , nghĩa là nồng độ c ngày càng tăng.
Chọn đáp án B.
NG
1
DD
26 tháng 3 2016
a) Áp dụng bất đẳng thức Cauchy cho các số dương, ta có :
\(\log_23+\log_32>2\sqrt{\log_23.\log_32}=2\sqrt{1}=2\)
Không xảy ra dấu "=" vì \(\log_23\ne\log_32\)
Mặt khác, ta lại có :
\(\log_23+\log_32<\frac{5}{2}\Leftrightarrow\log_23+\frac{1}{\log_23}-\frac{5}{2}<0\)
\(\Leftrightarrow2\log^2_23-5\log_23+2<0\)
\(\Leftrightarrow\left(\log_23-1\right)\left(\log_23-2\right)<0\) (*)
Hơn nữa, \(2\log_23>2\log_22>1\) nên \(2\log_23-1>0\)
Mà \(\log_23<\log_24=2\Rightarrow\log_23-2<0\)
Từ đó suy ra (*) luôn đúng. Vậy \(2<\log_23+\log_32<\frac{5}{2}\)
b) Vì \(a,b\ge1\) nên \(\ln a,\ln b,\ln\frac{a+b}{2}\) không âm.
Áp dụng bất đẳng thức Cauchy ta có
\(\ln a+\ln b\ge2\sqrt{\ln a.\ln b}\)
Suy ra
\(2\left(\ln a+\ln b\right)\ge\ln a+\ln b+2\sqrt{\ln a\ln b}=\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
Mặt khác :
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\ln\frac{a+b}{2}\ge\frac{1}{2}\left(\ln a+\ln b\right)\)
Từ đó ta thu được :
\(\ln\frac{a+b}{2}\ge\frac{1}{4}\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
hay \(\frac{\sqrt{\ln a}+\sqrt{\ln b}}{2}\le\sqrt{\ln\frac{a+b}{2}}\)
c) Ta chứng minh bài toán tổng quát :
\(\log_n\left(n+1\right)>\log_{n+1}\left(n+2\right)\) với mọi n >1
Thật vậy,
\(\left(n+1\right)^2=n\left(n+2\right)+1>n\left(n+2\right)>1\)
suy ra :
\(\log_{\left(n+1\right)^2}n\left(n+2\right)<1\Leftrightarrow\frac{1}{2}\log_{n+1}n\left(n+2\right)<1\)
\(\Leftrightarrow\log_{n+1}n+\log_{\left(n+1\right)}n\left(n+2\right)<2\)
Áp dụng bất đẳng thức Cauchy ta có :
\(2>\log_{\left(n+1\right)}n+\log_{\left(n+1\right)}n\left(n+2\right)>2\sqrt{\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)}\)
Do đó ta có :
\(1>\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)\) và \(\log_n\left(n+1>\right)\log_{\left(n+1\right)}\left(n+2\right)\) với mọi n>1
Quy tắc tính logarit