Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí: Mỗi đa giác đều có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

Sửa đề: Hai đường cao BN,CK
a: góc AKH+góc ANH=180 độ
=>AKHN nội tiếp
Tâm là trung điểm của AH
b: Xet ΔANB vuông tại N và ΔAKC vuông tại K có
góc A chung
=>ΔANB đồng dạng với ΔAKC
=>NB/KC=AN/AK
=>NB*AK=AN*KC
c: góc BKC=góc BNC=90 độ
=>BKNC nội tiếp
d: Xét ΔACB co
BN,CK là đường cao
BN cắt CK tại H
=>H là trực tâm
=>AH vuông góc CB

Ta có \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BCEF nội tiếp đường tròn đường kính BC. Tâm I của đường tròn này là trung điểm của BC

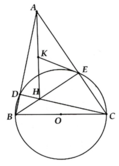
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
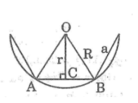
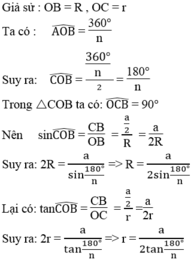
Định lí: Mỗi đa giác đều có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.