Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x-\sqrt{x}\) \(\left(ĐKXĐ:x\ge0\right)\)
\(A=x-2.\sqrt{x}.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
\(A=\left(x-\frac{1}{2}\right)^2\) \(-\frac{1}{4}\)
Có \(\left(x-\frac{1}{2^2}\right)\ge0\forall x\ge0\)
\(\left(x-\frac{1}{2}\right)^2\) - 1/4 >= \(\frac{-1}{4}\)mọi x>=0
Dấu = sảy ra \(\Leftrightarrow\) x- \(\frac{1}{2}\) = 0
\(\Leftrightarrow\) x = 1 / 2 ( t/m )
vậy A đạt GTNN là -1/4 tại x = 1/2
Tớ nhầm nhé \(x\) từ dòng thứ 3 xuống pahir thay =\(\sqrt{x}\)

X1².X2² = (X1.X2)² = (\(\dfrac{c}{a}\) )2 =\(\dfrac{c^2}{a^2}\)
Hệ thức Vi-ét: X1.X2 = \(\dfrac{c}{a}\)

Làm sai thì thôi nha!
ĐK: x>=0 \(A=x-2.\sqrt{x}.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
\(=\left(\sqrt{x}-\frac{1}{2}\right)^2-\frac{1}{4}\ge-\frac{1}{4}\)
đẳng thức xảy ra khi x = 1/4
A=\(x-\sqrt{x}=x-2\times\sqrt{x}\times\frac{1}{2}+\frac{1}{4}-\frac{1}{4}=(\sqrt{x}-\frac{1}{2})^2+\frac{1}{4}\ge\frac{1}{4}\)
GTNN A=\(\frac{1}{4}\Leftrightarrow\sqrt{x}-\frac{1}{2}=0\Leftrightarrow\sqrt{x}=\frac{1}{2}\Leftrightarrow x=\frac{1}{4}\)

+ Delta là một chữ cái trong bảng chữ Hy Lạp, được kí hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường).
+ Trong toán học, đặc biệt là Toán 9, ký hiệu Δ chỉ một biệt thức trong phương trình bậc hai mà dựa vào từng giá trị của delta ta có thể kết luận được số nghiệm của phương trình bậc hai.
+ Ngoài ra delta còn dùng để kí hiệu cho đường thẳng mà các bạn sẽ được học ở các lớp cao hơn.

Ta có: ∆ ’ = 3 2 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có: 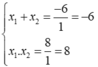
Giải ra ta được x 1 = -2, x 2 = -4
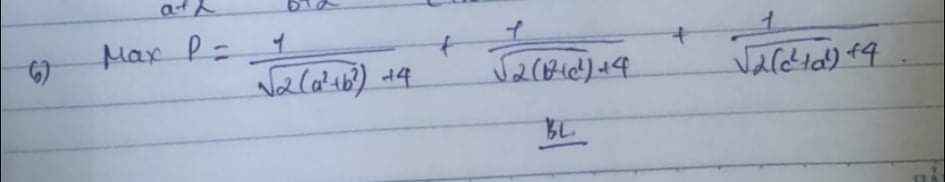 mọi người giúp em với ạ😁😁😁
mọi người giúp em với ạ😁😁😁
\(x^3_1-x_2^3=\left(\left(x_1-x_2\right)\left(x^2_1+x_1x_2+x_2^2\right)=\left(x_1-x_2\right)\left[\left(x_1+x_2\right)\right]^2-x_1x_2=......\right)\)