Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(\frac{3}{x^2-4y^2}\)
\(=\frac{3}{\left(x-2y\right)\left(x+2y\right)}\)
Phân thức xác định khi \(\left(x-2y\right)\left(x+2y\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x-2y\ne0\\x+2y\ne0\end{cases}}\Rightarrow x\ne\pm2y\)
2) \(\frac{2x}{8x^3+12x^2+6x+1}\)
\(=\frac{2x}{\left(2x+1\right)^3}\)
Phân thức xác định khi \(\left(2x+1\right)^3\ne0\)
\(\Rightarrow2x+1\ne0\)
\(\Rightarrow x\ne-\frac{1}{2}\)
3) \(\frac{5}{2x-3x^2}\)
\(=\frac{5}{x\left(2-3x\right)}\)
Phân thức xác định khi : \(x\left(2-3x\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\2-3x\ne0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\x\ne\frac{2}{3}\end{cases}}\)

\(a,ĐK:x^2-1=\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne\pm1\\ \dfrac{3x+3}{x^2-1}=\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x-1}=2\\ \Leftrightarrow x-1=\dfrac{3}{2}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\\ b,\dfrac{3}{x-1}\in Z\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\left(tm\right)\)

\(P=\dfrac{3x^2+6x+3}{x+1}\)
\(a,\) Điều kiện xác định: \(x+1\ne0\Leftrightarrow x\ne-1\)
\(b,P=\dfrac{3x^2+6x+3}{x+1}=\dfrac{3\left(x^2+2x+1\right)}{x+1}=\dfrac{3\left(x+1\right)^2}{x+1}=3\left(x+1\right)=3x+3\)
\(c,x=1\Rightarrow P=3.1+3=6\)
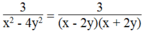
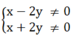 ⇒ x
≠
±
2y
⇒ x
≠
±
2y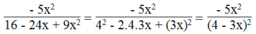

x(2 – 3x) ≠ 0 ⇔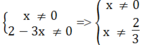
Vậy phân thức 5 2 x - 3 x 2 xác định với x ≠ 0 và x ≠ 2/3