LD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 10 2017
x 2 y + x y 2 + x 2 z + x z 2 + y 2 z + y z 2 + 3xyz.
= ( x 2 y + x 2 z + xyz) + (x y 2 + y 2 z + xyz) + (x z 2 + y z 2 + xyz)
= x(xy + xz + yz) + y(xy + yz + xz) + z(xz + yz + xy)
= (x + y + z)(xy + xz + yz).
NC
14 tháng 12 2020
\(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)
\(=\left(x^2y+x^2z+xyz\right)+\left(xz^2+yz^2+xyz\right)+\left(xy^2+y^2z+xyz\right)\)
\(=x\left(xy+xz+yz\right)+z\left(xz+yz+xy\right)+y\left(xy+yz+xz\right)\)
\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)
MH
25 tháng 10 2021
a) \(3x\left(2x-y\right)+5y\left(y-2x\right)\)
\(=3x\left(2x-y\right)-5y\left(2x-y\right)\)
\(=\left(3x-5y\right)\left(2x-y\right)\)
b) \(\left(x-5\right)^2-9\left(x+y\right)^2\)
\(=\left(x-5\right)^2-3^2\left(x+y\right)^2\)
\(=\left(x-5\right)^2-\left(3x+3y\right)^2\)
\(=\left(x-5+3x+3y\right)\left(x-5-3x-3y\right)\)
\(=\left(4x+3y-5\right)\left(-2x-3y-5\right)\)
25 tháng 10 2021
a: \(3x\left(2x-y\right)+5y\left(y-2x\right)=\left(2x-y\right)\left(3x-5y\right)\)
e: \(x^2-10x+24=\left(x-4\right)\left(x-6\right)\)
TL
1
DL
1
3 tháng 8 2021
a) \(4x^2-9y^2+6x-9y\)
\(=\left(2x-3y\right)\left(2x+3y\right)+3\left(2x-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+3\right)\)
b) \(1-2x+2yz+x^2-y^2-z^2\)
\(=\left(x^2-2x+1\right)-\left(y^2-2yz+z^2\right)\)
\(=\left(x-1\right)^2-\left(y-z\right)^2\)
\(=\left(x-y+z-1\right)\left(x+y-z-1\right)\)
Tick hộ mình nha 😘
PT
1
23 tháng 8 2021
\(A=x\left(y^2-z^2\right)+y\left(z^2-x^2\right)+z\left(x^2-y^2\right)=x\left(y^2-z^2\right)+y\left(-y^2+z^2-x^2+y^2\right)+z\left(x^2-y^2\right)=\left(y^2-z^2\right)\left(x-y\right)+\left(x^2-y^2\right)\left(z-y\right)=\left(y-z\right)\left(y+z\right)\left(x-y\right)-\left(x-y\right)\left(x+y\right)\left(y-z\right)=\left(x-y\right)\left(y-z\right)\left(y+z-x-y\right)=\left(x-y\right)\left(y-z\right)\left(z-x\right)\)
23 tháng 8 2021
\(B=a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)=ab^3-ac^3+bc^3-a^3b+a^3c-b^3c=ab\left(b^2-a^2\right)-c^3\left(a-b\right)+c\left(a^3-b^3\right)=-ab\left(a-b\right)\left(a+b\right)-c^3\left(a-b\right)+c\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)\left(-a^2b-ab^2-c^3+a^2c+abc+b^2c\right)\)
NT
0
5 tháng 9 2021
\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11
5 tháng 9 2021
e: Ta có: \(x^2-6x+y^2+4y+2=0\)
\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Dấu '=' xảy ra khi x=3 và y=-2
16 tháng 11 2021
\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
16 tháng 11 2021
Câu 1
a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)
b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)
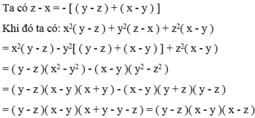
\(A=x\left(y^2-z^2\right)+y\left(z^2-x^2\right)+z\left(x^2-y^2\right)\)
\(=x\left(y-z\right)\left(y+z\right)+yz^2-yx^2+zx^2-zy^2\)
\(=\left(y-z\right)\left[x.\left(y+z\right)\right]-x^2\left(y-z\right)-yz\left(y-z\right)\)
\(=\left(y-z\right)\left(xy+xz\right)-x^2\left(y-z\right)-yz\left(y-z\right)\)
\(=\left(y-z\right)\left(xy+xz-x^2-yz\right)\)
\(=\left(y-z\right)\left[\left(xy-x^2\right)+\left(xz-yz\right)\right]\)
\(=\left(y-z\right)\left[x\left(y-x\right)-z\left(y-x\right)\right]\)
\(=\left(y-z\right)\left(y-x\right)\left(x-z\right)\)