K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
23 tháng 4 2017
\(f\left(x\right)=9-3x^3-2x^3+x^2+4x-6\)
\(g\left(x\right)=x^3-6x^3+2x^3+4x^2+7x-3x+3\)
\(\Rightarrow f\left(x\right)-g\left(x\right)=9-3x^3-2x^3+x^2+4x-6-\left(x^3-6x^3+2x^3+4x^2+7x-3x+3\right)\)
Bạn tự phá dấu và trừ ra nhé, ghi ở đây dài lắm, kết quả bằng :
\(-2x^3-3x^2\)
HQ
23 tháng 4 2017
Ta có:
\(f\left(x\right)=-5x^3+x^2+4x+3\)
\(g\left(x\right)=-3x^3+4x^2+4x+3\)
NT
2
15 tháng 2 2017
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó
VH
0
28 tháng 4 2017
Chắc cậu giải được câu a) rồi nhỉ ?
Mình giải câu b) nha.
P(x)=-Q(x)\(\Rightarrow\)3x3+x2-3x+7=3x3+x2+x+15
-3x+7= x+15
-4x =8
x =-2
Vậy x=-2 để P(x)=-Q(x)
Chúc bạn học tốt
.
XE
1
8 tháng 5 2017
\(A\left(x\right)=-2x^2+x-3\)
\(=-\left(2x^2-x+3\right)=-2\left(x^2-\dfrac{x}{2}+\dfrac{3}{2}\right)\)
\(=-2\left(x^2-\dfrac{x}{2}+\dfrac{1}{16}+\dfrac{23}{16}\right)\)
\(=-2\left(x^2-\dfrac{x}{2}+\dfrac{1}{16}\right)-\dfrac{23}{8}\)
\(=-2\left(x-\dfrac{1}{4}\right)^2-\dfrac{23}{8}\le-\dfrac{23}{8}< 0\) ( vô nghiệm )
2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)
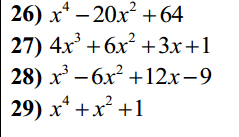
26) Ta có: \(x^4-20x^2+64\)
\(=x^4-16x^2-4x^2+64\)
\(=x^2\left(x^2-16\right)-4\left(x^2-16\right)\)
\(=\left(x-4\right)\left(x+4\right)\left(x-2\right)\left(x+2\right)\)
27) Ta có: \(4x^3+6x^2+3x+1\)
\(=4x^3+4x^2+2x^2+2x+x+1\)
\(=4x^2\left(x+1\right)+2x\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(4x^2+2x+1\right)\)
28) Ta có: \(x^3-6x^2+12x-9\)
\(=x^3-3x^2-3x^2+9x+3x-9\)
\(=x^2\cdot\left(x-3\right)-3x\left(x-3\right)+3\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-3x+3\right)\)
29: Ta có: \(x^4+x^2+1\)
\(=x^4+2x^2+1-x^2\)
\(=\left(x^2+1\right)^2-x^2\)
\(=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
26) Ta có: x4−20x2+64x4−20x2+64
=x4−16x2−4x2+64=x4−16x2−4x2+64
=x2(x2−16)−4(x2−16)=x2(x2−16)−4(x2−16)
=(x−4)(x+4)(x−2)(x+2)=(x−4)(x+4)(x−2)(x+2)
27) Ta có: 4x3+6x2+3x+14x3+6x2+3x+1
=4x3+4x2+2x2+2x+x+1=4x3+4x2+2x2+2x+x+1
=4x2(x+1)+2x(x+1)+(x+1)=4x2(x+1)+2x(x+1)+(x+1)
=(x+1)(4x2+2x+1)=(x+1)(4x2+2x+1)
28) Ta có: x3−6x2+12x−9x3−6x2+12x−9
=x3−3x2−3x2+9x+3x−9=x3−3x2−3x2+9x+3x−9
=x2⋅(x−3)−3x(x−3)+3(x−3)=x2⋅(x−3)−3x(x−3)+3(x−3)
=(x−3)(x2−3x+3)=(x−3)(x2−3x+3)
29: Ta có: x4+x2+1x4+x2+1
=x4+2x2+1−x2=x4+2x2+1−x2
=(x2+1)2−x2=(x2+1)2−x2
=(x2−x+1)(x2+x+1)