Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(xy\left(a^2+2b^2\right)-ab\left(2x^2+y^2\right)\)
\(=a^2xy+2b^2xy-2abx^2-aby^2\)
\(=\left(a^2xy-aby^2\right)+\left(2b^2xy-2abx^2\right)\)
\(=ay\left(ax-by\right)+2bx\left(by-ax\right)\)
\(=ay\left(ax-by\right)-2bx\left(ax-by\right)\)
\(=\left(ax-by\right)\left(ay-2bx\right)\)
2) Sửa đề \(\left(xy+ab\right)^2+\left(bx-ay\right)^2\)
\(=\left(xy\right)^2+2xyab+\left(ab\right)^2+\left(bx\right)^2-2xyab+\left(ay\right)^2\)
\(=x^2y^2+a^2b^2+b^2x^2+a^2y^2\)
\(=\left(x^2y^2+b^2x^2\right)+\left(a^2b^2+a^2y^2\right)\)
\(=x^2\left(b^2+y^2\right)+a^2\left(b^2+y^2\right)\)
\(=\left(b^2+y^2\right)\left(x^2+a^2\right)\)
3) \(\left(2xy+ab\right)^2+\left(2ay-bx\right)^2\)
\(=\left(2xy\right)^2+2.2xyab+\left(ab\right)^2+\left(2ay\right)^2-2.2xyab+\left(bx\right)^2\)
\(=4x^2y^2+4xyab+a^2b^2+4a^2y^2-4xyab+b^2x^2\)
\(=4x^2y^2+4a^2y^2+a^2b^2+b^2x^2\)
\(=4y^2\left(x^2+a^2\right)+b^2\left(a^2+x^2\right)\)
\(=\left(a^2+x^2\right)\left(4y^2+b^2\right)\)

Phân tích đa thức thành nhân tử ( phối hợp các phương pháp )
1) x2 - ( a + b )xy + aby2
\(=x^2-axy-bxy+aby^2\)
\(=(x^2-axy)-(bxy+aby^2)\)
\(=x(x-ay)-by(x+ay)\)
\(=(x-ay)(x-by)\)
2) x2 + ( 2a + b )xy + 2aby2
=x2 + 2axy + bxy + 2aby2
=(x2+ bxy) +(2axy+ 2aby2 )
=x(x+ by) +2ay(x+ by)
=(x+ by)(x+2ay)

a) \(2x-72x^3=2x\left(1-36x^2\right)=2x\left(1-6x\right)\left(1+6x\right)\)
f) \(4x^4+1=4x^4+4x^2+1-4x^2=\left(2x^2+1\right)^2-\left(2x\right)^2=\left(2x^2-2x+1\right)\left(2x^2+2x+1\right)\)

\(ax+bx+ay+by\)
\(=x\left(a+b\right)+y\left(a+b\right)\)
\(=\left(x+y\right)\left(a+b\right)\)
\(xy+1-x-y\)
\(=x\left(y-1\right)-\left(y-1\right)\)
\(=\left(x-1\right)\left(y-1\right)\)

Bài 4:
Ta có: \(\left(x^3-x^2\right)-4x^2+8x-4=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

1. \(xy\left(a^2+2b^2\right)-ab\left(2x^2+y^2\right)\)
\(=xya^2+2xyb^2-2abx^2-aby^2\)
\(=xya^2-aby^2-2abx^2+2xyb^2\)
\(=ay\left(ax-by\right)-2bx\left(ax-by\right)\)
\(=\left(ay-2bx\right)\left(ax-by\right)\)
2. \(xy\left(a^2+2b^2\right)+ab\left(2x^2+y^2\right)\)
\(=xya^2+2xyb^2+2abx^2+aby^2\)
\(=xya^2+aby^2+2abx^2+2xyb^2\)
\(=ay\left(ax+by\right)+2bx\left(ax+by\right)\)
\(=\left(ay+2bx\right)\left(ax+by\right)\)

\(=x^2y^2+8xyab+16a^2b^2+4a^2y^2-8xyab+4b^2x^2\)
\(=x^2y^2+4a^2y^2+4b^2x^2+16a^2b^2\)
\(=\left(x^2y^2+4b^2x^2\right)+\left(4a^2y^2+16a^2b^2\right)\)
\(=x^2\left(4b^2+y^2\right)+4a^2\left(y^2+4b^2\right)\)
\(=\left(4b^2+y^2\right)\left(x^2+4a^2\right)\)

\(\left(xy+4ab\right)^2+4\left(ay-bx\right)^2\)
\(=x^2y^2+8abxy+16a^2b^2+4a^2y^2-8abxy+4b^2x^2\)
\(=x^2y^2+16a^2b^2+4a^2y^2+4b^2x^2\)
\(=\left(x^2y^2+4b^2x^2\right)+\left(16a^2b^2+4a^2y^2\right)\)
\(=x^2\left(y^2+4b^2\right)+4a^2\left(4b^2+y^2\right)\)
\(=\left(x^2+a^2\right)\left(4b^2+y^2\right)\)

\(\left(xy+4ab\right)^2+4\left(ay-bx\right)^2\)
\(=x^2y^2+2xy.4ab+4^2a^2b^2+4\left(a^2y^2-2aybx+b^2x^2\right)\)
\(=x^2y^2+8aybx+16a^2b^2+4a^2y^2-8aybx+4b^2x^2\)
\(=x^2y^2+16a^2b^2+4a^2y^2+4b^2x^2\)
\(=\left(x^2y^2+4b^2x^2\right)+\left(16a^2b^2+4a^2y^2\right)\)
\(=x^2\left(y^2+4b^2\right)+4a^2\left(4b^2+y^2\right)\)
\(=\left(y^2+4b^2\right)\left(x^2+4a^2\right)\)
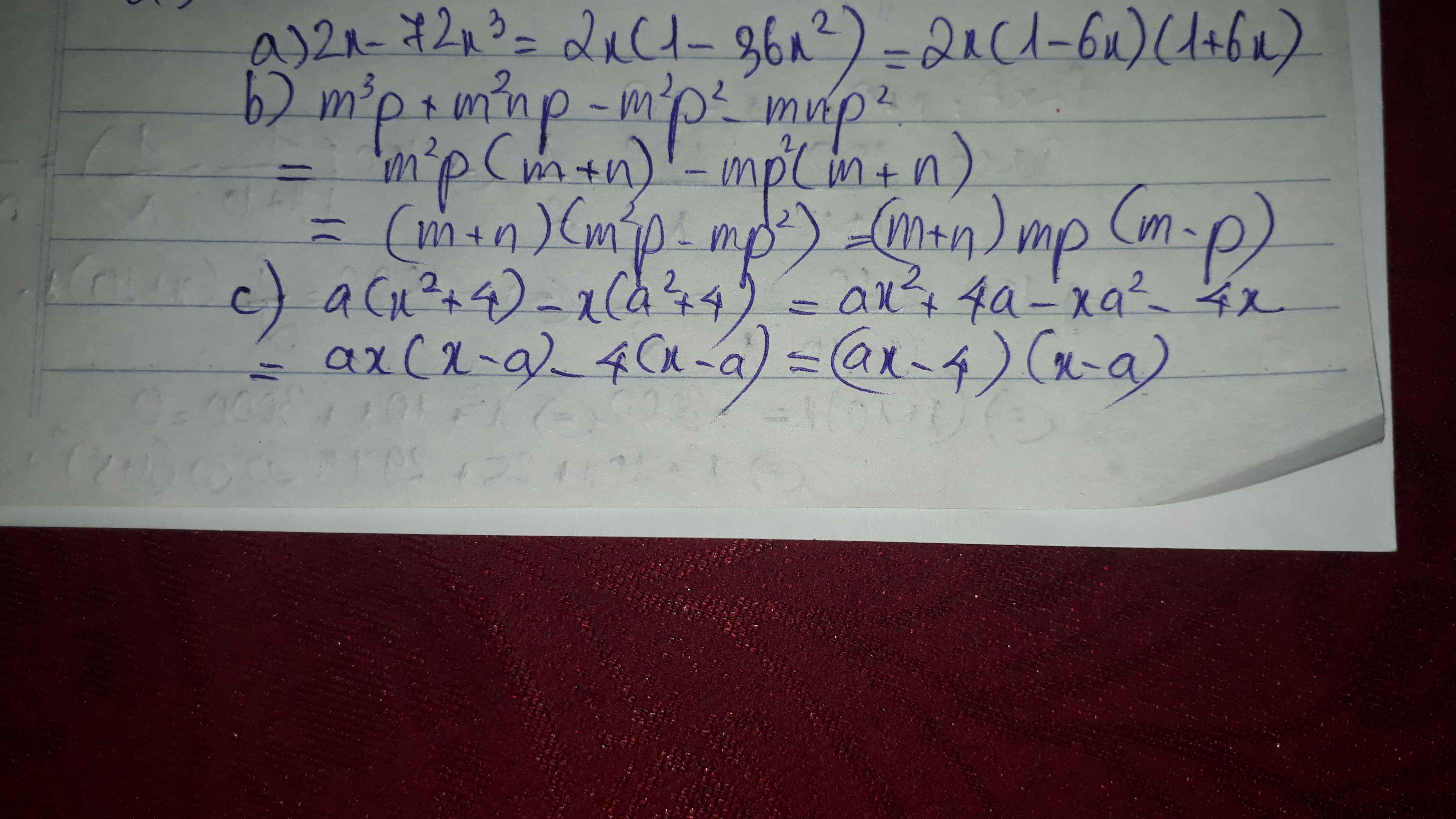

1) \(xy\left(a^2+2b^2\right)-ab\left(2x^2+y^2\right)\)
\(=a^2xy+2b^2xy-2x^2ab-y^2ab\)
\(=\left(a^2xy-y^2ab\right)+\left(2b^2xy-2x^2ab\right)\)
\(=ay\left(ax-by\right)+2bx\left(by-ax\right)\)
\(=ay\left(ax-by\right)-2bx\left(ax-by\right)\)
\(=\left(ax-by\right)\left(ay-2bx\right)\)
2) Sửa đề \(\left(xy+ab\right)^2+\left(bx-ay\right)^2\)
\(=\left(xy\right)^2+2xyab+\left(ab\right)^2+\left(bx\right)^2-2xyab+\left(ay\right)^2\)
\(=x^2y^2+a^2b^2+b^2x^2+a^2y^2\)
\(=\left(x^2y^2+b^2x^2\right)+\left(a^2b^2+a^2y^2\right)\)
\(=x^2\left(b^2+y^2\right)+a^2\left(b^2+y^2\right)\)
\(=\left(b^2+y^2\right)\left(a^2+x^2\right)\)
3) \(\left(2xy+ab\right)^2+\left(2ay-bx\right)^2\)
\(=\left(2xy\right)^2+2.2xyab+\left(ab\right)^2+\left(2ay\right)^2-2.2xyab+\left(bx\right)^2\)
\(=4x^2y^2+a^2b^2+4a^2y^2+b^2x^2\)
\(=\left(4x^2y^2+b^2x^2\right)+\left(4a^2y^2+a^2b^2\right)\)
\(=x^2\left(4y^2+b^2\right)+a^2\left(4y^2+b^2\right)\)
\(=\left(4y^2+b^2\right)\left(a^2+x^2\right)\)