
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(x\sqrt{y}+y\sqrt{x}=\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)\)
2) \(9-6\sqrt{a}+a=\left(\sqrt{a}-3\right)^2\)
3) \(a+2\sqrt{ab}+b=\left(\sqrt{a}+\sqrt{b}\right)^2\)
4) \(x-y+\sqrt{x}+\sqrt{y}=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)+\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}+1\right)\)
5) \(a+2\sqrt{ab}+b-1=\left(\sqrt{a}+\sqrt{b}\right)^2-1=\left(\sqrt{a}+\sqrt{b}-1\right)\left(\sqrt{a}+\sqrt{b}+1\right)\)
1) \(x\sqrt{y}+y\sqrt{x}=\sqrt{x}\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)\)
2) \(9-6\sqrt{a}+a=\left(3-\sqrt{a}\right)^2\)
3) \(a+2\sqrt{ab}+b=\left(\sqrt{a}+\sqrt{b}\right)^2\)
4) \(x-y+\sqrt{x}+\sqrt{y}=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)+\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}+1\right)\)
5) \(a+2\sqrt{ab}+b-1=\left(\sqrt{a}+\sqrt{b}\right)^2-1^2=\left(\sqrt{a}+\sqrt{b}-1\right)\left(\sqrt{a}+\sqrt{b}+1\right)\)

i) \(=x\left(x-5\right)+3\left(x-5\right)=\left(x-5\right)\left(x+3\right)\)
j) \(=x\left(x-1\right)+8\left(x-1\right)=\left(x-1\right)\left(x+8\right)\)
k) \(=x\left(x+1\right)+3\left(x+1\right)=\left(x+1\right)\left(x+3\right)\)
l) \(=x\left(x-3\right)-2\left(x-3\right)=\left(x-3\right)\left(x-2\right)\)
m) \(=x\left(x^2-4x+4\right)=x\left(x-2\right)^2\)

\(=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-1-y\right)\left(x-1+y\right)\)

3: \(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}=\sqrt{5}-\sqrt{3}\)
4: \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)

12) \(\sqrt{11+2\sqrt{30}}=\sqrt{\left(\sqrt{6}\right)^2+2.\sqrt{6}.\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}=\sqrt{6}+\sqrt{5}\)
\(=\sqrt{6+2\cdot\sqrt{6}\cdot\sqrt{5}+5}\)
\(=\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}=\sqrt{6}+\sqrt{5}\)

\(\Delta=27^2-4.168=57>0\)
pt có 2 nghiệm pb
\(x=\dfrac{27\pm\sqrt{57}}{2}\)


`x^2-x-2001.2002`
`=x^2-2002x+2001x-2001.2002`
`=x(x-2002)+2001(x-2002)`
`=(x-2002)(x+2001)`.
x2 - x - 2001.2002
= (x2 - 2002x) + (2001x - 2001.2002)
= x(x - 2002) + 2001(x - 2002)
= (x + 2001)(x- 2002)

\(=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
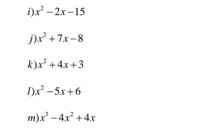
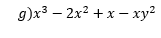
 phân tích đa thức thành nhân tử
phân tích đa thức thành nhân tử phân tích đa thức thành nhân tử ạ
phân tích đa thức thành nhân tử ạ phân tích đa thức thành nhân tử vs ạ
phân tích đa thức thành nhân tử vs ạ