K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
2
2 tháng 4 2018
a^3+b^3+6ab-8=(a + b - 2) (a² - a b + 2a + b² + 2b + 4)
DN
1
PA
15 tháng 9 2016
4a2b2 + 36a2b3 + 6ab4
= 2ab2(2a + 18ab + 3b2)
4a2b3 - 6a3b2
= 2a2b2(2b - 3a)
G
0
TM
2
19 tháng 7 2019
\(A=9a^2-6ab+b^2-1\)
\(A=\left(3a-b\right)^2-1\)
\(A=\left(3a-b-1\right)\left(3a-b+1\right)\)
P/s haphuong
2 tháng 8 2021
\(9a^2b+6ab^2+b^3-6ab-2b^2\)
\(=b\left(9a^2+6ab+b^2-6a-2b\right)\)
\(=b\left[\left(3a+b\right)^2-2\left(3a+b\right)\right]\)
\(=b\left(3a+b\right)\left(3a+b-2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2021
\(=b\left(9a^2+6ab+b^2\right)-2b\left(3a+b\right)\)
\(=b\left(3a+b\right)^2-2b\left(3a+b\right)\)
\(=b\left(3a+b\right)\left(3a+b-2\right)\)
2 tháng 8 2021
\(9a^2b+6ab^2+b^3-6ab-2b^2\)
\(=b\left(9a^2+6ab+b^2-6a-2b\right)\)
\(=b\left[\left(3a+b\right)^2-2\left(3a+b\right)\right]\)
\(=b\left(3a+b\right)\left(3a+b-2\right)\)
HB
3
10 tháng 9 2021
Đặt `a+b=x, b+c=y, c+a=z`
`->x+y+z=2 (a+b+c)`
`(a+b)^3 +(b+c)^3 + (c+a)^3 - 8 (a+b+c)^3`
`= x^3 + y^3 + z^3 - 2^3 (a+b+c)^3`
`=x^3 +y^3 +z^3 - [2 (a+b+c)]^3`
`=x^3 +y^3+z^3 - (x+y+z)^3`
`= x^3 + y^3 +z^3 - [x^3 +y^3 +z^3 + 3 (x+y) (y+z) (x+z)]`
`= -3 (x+y)(y+z)(x+z)`
`= -3 (2b + a+c) (2c+a+b) (2a +b+c)`
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 9 2021
Đặt : \(\hept{\begin{cases}a+b=x\\b+c=y\\c+a=z\end{cases}}\Rightarrow\left(a+b\right)^3+\left(b+c\right)^3+\left(a+c\right)^3-8\left(a+b+c\right)^3=x^3+y^3+z^3-\left(x+y+z\right)^3\)
\(=x^3+y^3+z^3-\left(x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)\right)=-3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(=-3\left(2a+b+c\right)\left(a+2b+c\right)\left(a+b+2c\right)\)
a^3+b^3+6ab-8=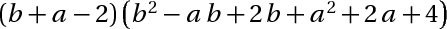
\(\left(a+b-2\right)\left(b^2-ab+2b+a^2+2a+4\right)\)