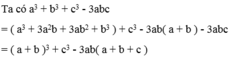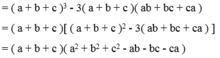H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
0
12 tháng 10 2021
\(a,a^2\left(a-b\right)+ab\left(a-c\right)=a\left(a+b\right)\left(a-c\right)\\ c,=\left(x^2-2x+1\right)\left(x^2+2x+1\right)=\left(x-1\right)^2\left(x+1\right)^2\\ b,=\left(x-5\right)^2-9y^2=\left(x-5-3y\right)\left(x-5+3y\right)\\ d,=4\left(x^2-9x+14\right)=4\left(x-7\right)\left(x-2\right)\)
CM
19 tháng 4 2019
Ta có
a 4 + a 3 + a 3 b + a 2 b = a 4 + a 3 + a 3 b + a 2 b = a 3 a + 1 + a 2 b a + 1 = a + 1 a 3 + a 2 b = a + 1 a 2 a + b = a 2 a + b a + 1
Đáp án cần chọn là: A
C
1
4 tháng 8 2021
a) \(45a^3-30a^2+5a-500=5\left(9a^3-6a^2+a-100\right)\)
b) \(a^2b-49b+14b^2-b^3=b\left(a^2-b^2+14b-49\right)=b\left[a^2-\left(b-7\right)^2\right]=b\left(a-b+7\right)\left(a+b-7\right)\)
Tick hộ tui nha 😘
3 tháng 8 2021
a) $7a^3 - 28a^2 + 28a$
$ = 7a.(a^2 - 4a+4)$
$ = 7a.(a-2)^2$
d) $x^4 + 4$
$ = (x^4+4x^2+4) - 4x^2$
$ = (x^2+2)^2 - (2x)^2$
$ = (x^2+2x+2)(x^2-2x+2)$
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
Do $a,b,c\in [0;1]$ nên:
$a^2(1-b)\leq 0$
$b^2(1-c)\leq 0$
$c^2(1-a)\leq 0$
Cộng theo vế suy ra: $a^2+b^2+c^2\leq a^2b+b^2c+c^2a$
Ta có đpcm.
PT
1
TC
2
AM
25 tháng 6 2015
Thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
Biến đổi vế trái thành:
a^3+b^3+c^3-3abc
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)