NN
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
6 tháng 7 2017
x 4 - 5 x 2 + 4 = x 4 - 4 x 2 - x 2 + 4 = x 4 - 4 x 2 - x 2 - 4 = x 2 x 2 - 4 - x 2 - 4 = x 2 - 4 x 2 - 1 = x + 2 x - 2 x + 1 x - 1
2 tháng 1
*Đoán nghiệm sử dụng tính chất của đa thức:
Ta dễ dàng nhận thấy đa thức \(P\left(x\right)=x^3+4x^2-19x+24\) không có nghiệm là \(\pm1\).
Giả sử \(P\left(x\right)\) có nghiệm hữu tỉ dạng \(\dfrac{p}{q}\left(p,q\inℤ\right)\), không mất tổng quát giả sử \(q>0\). Khi đó \(p|24\), \(q|1\) \(\Rightarrow q=1\).
Khi đó do \(P\left(x\right)\) không có nghiệm là \(\pm1\) nên \(p\in\left\{\pm2,\pm3,\pm4;\pm6;\pm8;\pm12;\pm24\right\}\)
Thử lại, ta thấy không có số \(p\) nào thỏa mãn \(\dfrac{p}{q}\) là nghiệm của P(x). Vậy đa thức \(P\left(x\right)\) không có nghiệm hữu tỉ \(\Rightarrow\) \(P\left(x\right)\) không thể phân tích thành nhân tử.
* Chú ý rằng chỉ khi \(degP\left(x\right)\le3\) hoặc \(degP\left(x\right)⋮̸2\) thì từ P(x) không có nghiệm hữu tỉ mới suy ra được P(x) không phân tích được thành nhân tử nhé. Nếu \(\left\{{}\begin{matrix}degP\left(x\right)\ge4\\degP\left(x\right)⋮2\end{matrix}\right.\) thì chưa chắc điều này đã đúng. VD: Đa thức \(Q\left(x\right)=x^4+4\) không có nghiệm hữu tỉ (nó thậm chí còn không có nghiệm thực) nhưng ta vẫn có thể phân tích thành nhân tử như sau:
\(Q\left(x\right)=x^4+4=x^4+4x^2+4-4x^2\)
\(=\left(x^2+2\right)^2-\left(2x\right)^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
PT
1
CM
30 tháng 5 2018
45 + x 3 - 5 x 2 - 9 x = x 3 - 5 x 2 - 9 x - 45 = x 2 x - 5 - 9 x - 5 = x - 5 x 2 - 9 = x - 5 x - 3 x + 3
28 tháng 10 2021
Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)
8 tháng 7 2016
\(5x^2-19x-4=5x^2-20x+x-4\)
\(=\left(5x^2-20x\right)+\left(x-4\right)\)
\(=5x\left(x-4\right)+\left(x-4\right)\)
\(=\left(5x-1\right)\left(x-4\right)\)
8 tháng 7 2016
= 5x^2 + x - 20x - 4
= (5x^2 + x) - (20x + 4)
= x(5x+1) - 4 (5x + 1)
= (5x+1) (x - 4)
PT
1
CM
5 tháng 4 2018
5x2 (x – 2y)– 15x(x – 2y) = x.5x(x - 2y) - 3.5x(x - 2y)
= (x - 3).5x(x - 2y)
A
6 tháng 8 2023
\(\text{x^3 – 5x^2 + 8x – 4 }\)
\(\text{= x^3 – 4x^2 + 4x – x^2 + 4x – 4}\)
\(\text{= x( x^2 – 4x + 4 ) – ( x^2 – 4x + 4 )}\)
\(\text{= ( x – 1 ) ( x – 2 )^2}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 8 2023
\(x^3-5x^2+8x-4=x^3-x^2-4x^2+4x-4\\ =x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x^2-4x+4\right)\left(x-1\right)\\ =\left(x-2\right)^2\left(x-1\right)\)
TQ
1
9 tháng 2 2021
Ta có : \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
9 tháng 2 2021
Ta có: \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
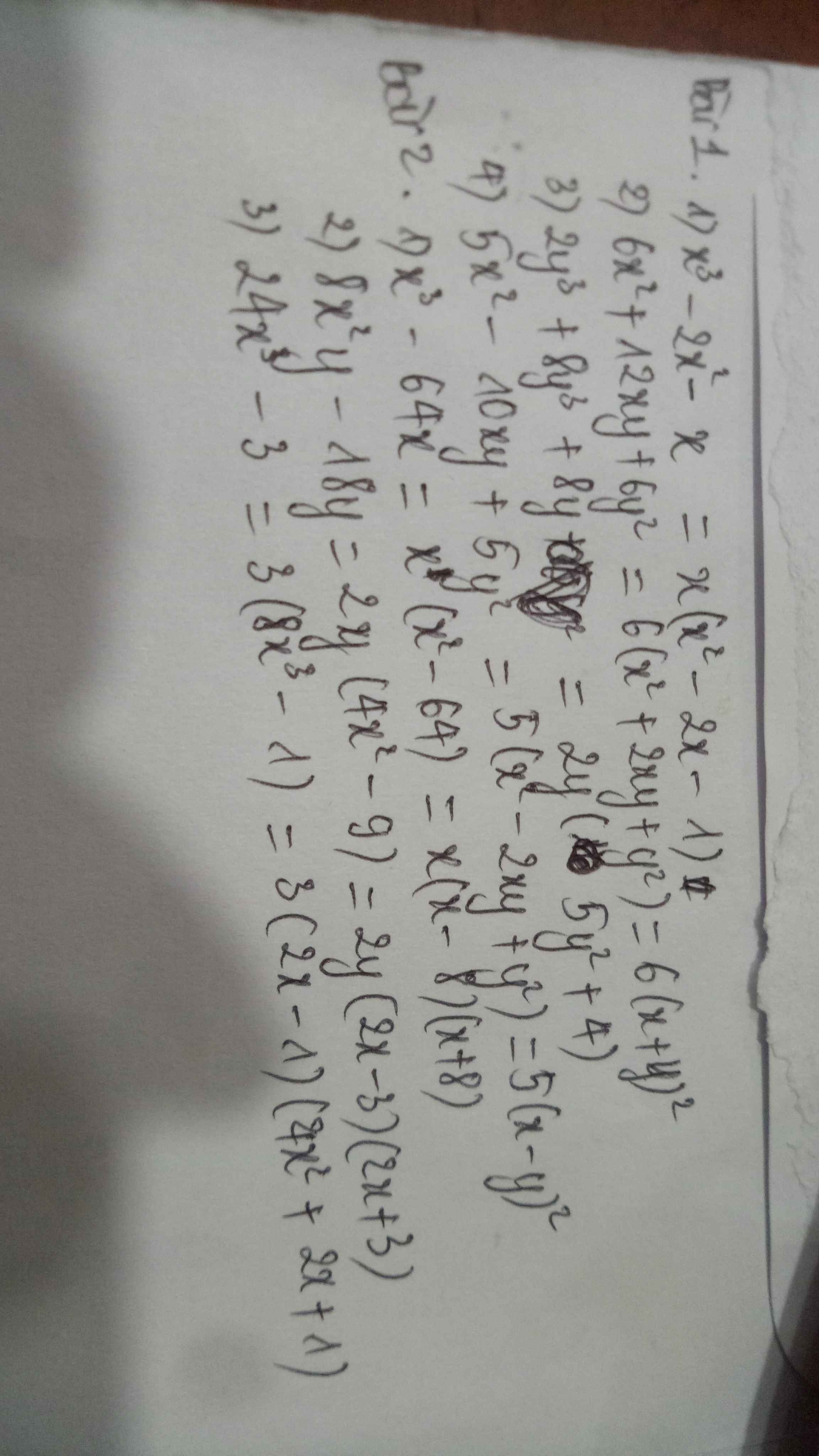
\(5x^2-19x-4\)
\(=\left(5x^2-20x\right)+\left(x-4\right)\)
\(=5x\left(x-4\right)+\left(x-4\right)\)
\(=\left(x-4\right)\left(5x+1\right)\)
\(5x^2-19x-4=5x^2+x-20x-4\)
\(=x\cdot\left(5x+1\right)-4\cdot\left(5x+1\right)\)
\(=\left(5x+1\right)\cdot\left(x-4\right)\)