
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x⁸ + x⁴ + 1
= x⁸ + 2x⁴ + 1 - x⁴
= (x⁴ + 1)² - x⁴
= (x⁴ + 1)² - (x²)²
= (x⁴ + 1 + x²)(x⁴ + 1 - x²)
= (x⁴ + x² + 1)(x⁴ - x² + 1)

\(\left(x-y\right)^3-\left(x+y\right)^3\\ =\left(x-y-x-y\right)\left(\left(x-y\right)^2+\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\right)\\ =-2y\left(x^2-2xy+y^2+x^2-y^2+x^2+2xy+y^2\right)\\ =-2y\left(3x^2+y^2\right)\)

\(\left(x-y\right)^3+\left(x+y\right)^3\\ =\left(x-y+x+y\right)\left(\left(x-y\right)^2-\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\right)\\ =2x\left(x^2-2xy+y^2-\left(x^2-y^2\right)+x^2+2xy+y^2\right)\\ =2x\left(x^2-2xy+y^2-x^2+y^2+x^2+2xy+y^2\right)\\ =2x\left(x^2+3y^2\right)\)

=(x-y-2y)[(x-y)^2+2y(x-y)+4y^2]
=(x-3y)(x^2-2xy+y^2+2xy-2y^2+4y^2)
=(x-3y)(x^2+3y^2)
\(\left(x-y\right)^3-8y^3\)
\(=\left(x-y\right)^3-\left(2y\right)^3\)
\(=\left[\left(x-y\right)-2y\right]\left[\left(x-y\right)^2+2y\left(x-y\right)+\left(2y\right)^2\right]\)
\(=\left(x-y-2y\right)\left(x^2-2xy+y^2+2xy-2y^2+4y^2\right)\)
\(=\left(x-3y\right)\left(x^2+3y^2\right)\)

a) Ta thay x=1 vào đa thức P(x) có:
P(1)= 1^3-3x1+2=-2+2=0
==> 1 là nghiệm của đa thức P(x)
Vậy 1 là nghiệm của đa thức P(x) (đbđcm)
b) bạn phân tích ra rồi đặt đa thức đó bằng 0 là ok
Ta có : P(1) = 13 - 3.1 + 2 = -2 + 2 = 0
Vậy x = 1 là 1 nghiệm của đa thức P(x)

Đặt \(x+y=u\)
Biểu thức trở thành \(u^2-8u+12\)
\(=u^2-2u-6u+12\)
\(=u\left(u-2\right)-6\left(u-2\right)\)
\(=\left(u-6\right)\left(u-2\right)\)
Thay ngược trở lại, ta được:
\(\left(x+y\right)^2-8\left(x+y\right)+12=\left(x+y-6\right)\left(x+y-2\right)\)
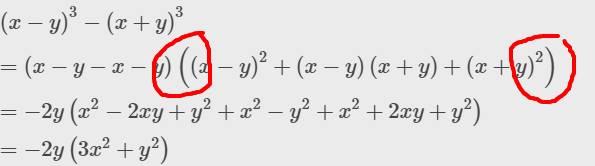
x3-x2+x+3=x3+1-x2+1+x+1
=(x+1)(x2+x+1)-(x2-1)+(x+1)
=(x+1)(x2+x+1)-(x+1)(x-1)+(x+1)
=(x+1)[(x2+x+1)-(x-1)+1]
=(x+1)(x2+x+1-x+1+1)
=(x+1)(x2+3)