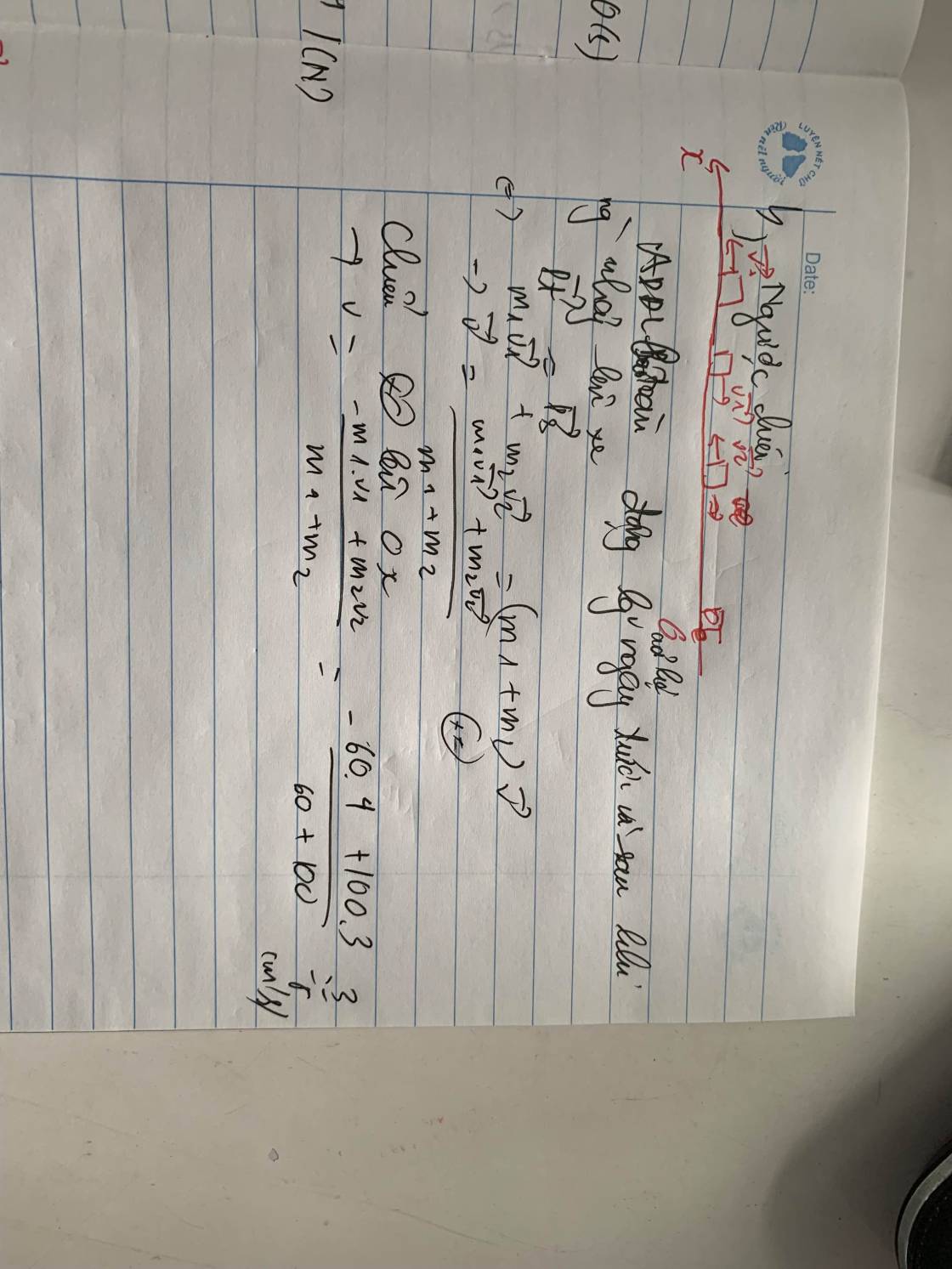Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xem hệ hai xe là hệ cô lập
- Áp dụng địmh luật bảo toàn động lượng của hệ.
\(m_1=v_1=\left(m_1+m_2\right)\overrightarrow{v}\)
\(\overrightarrow{v}\)cùng phương với vận tốc \(\overrightarrow{v_1}\)
Vận tốc của mỗi xe là:
\(v=\frac{m_1.v_1}{m_1+m_2}=1,45\left(m\text{/}s\right)\)

Áp dụng định luật bảo toàn động lượng :
→pt=→ps��→=��→ <=> m1→v1=m2→v2�1�1→=�2�2→
=> m1→v1+m2→v2=→v(m1+m2)�1�1→+�2�2→=�→(�1+�2)
<=> →v=m1→v1+m2→v2m1+m2�→=�1�1→+�2�2→�1+�2
chọn chiều dương là chiều chuyển động ban đầu của xe
a)Cùng chiều : v=60.4+3.10060+90=3,6(m/s)�=60.4+3.9060+90=3,4(�/�)
b) Ngược chiều : v=−60.4+3.10060+90=0,4(m/s)

Thiếu điều kiện: \(3m_1=m_2\)
Theo đề bài ta có: \(W_{đ1}=\dfrac{1}{7}W_{đ2}\)
\(\Rightarrow\dfrac{1}{2}m_1v^2_1=\dfrac{1}{7}.\dfrac{1}{2}m_2v_2^2\)
\(\Rightarrow v_2=1,53v_1\)
Nếu xe 1 giảm vận tốc đi 3m/s thì ta có \(W_{đ1}=W_{đ2}\)
\(\Rightarrow\dfrac{1}{2}m_1\left(v_1-3\right)^2=\dfrac{1}{2}m_2v_2^2\)
\(\Rightarrow\dfrac{3m_1\left(1,53v_1\right)}{2}\)
\(\Rightarrow v_1=0,82m/s;v_2=1,25m/s\)
Chọn A

a) Gọi m là khối lượng hàng hóa trên xe.
Theo đề bài, ta có: \(F=0,3\times1500=450N\)
lại có \(F=0,2\times\left(m+1500\right)\)= 450
giải phương trình trên, ta được m = 750 kg
==> Vậy khối lượng hàng hóa trên xe là 750 kg

Áp dụng định luật II Niu tơn ta có:
\(a=\dfrac{F}{m}\)
Suy ra:
\(a_1=\dfrac{F}{m_1}\)
\(a_2=\dfrac{F}{m_2}\)
Ta cần tìm:
\(a_3=\dfrac{F}{m_3}=\dfrac{F}{m_1+m_2}\)
\(\Rightarrow \dfrac{1}{a_3}=\dfrac{m_1+m_2}{F}=\dfrac{m_1}{F}+\dfrac{m_2}{F}\)
\(\Rightarrow \dfrac{1}{a_3}=\dfrac{1}{a_1}+\dfrac{1}{a_2}\)
\(\Rightarrow a_3=\dfrac{a_1.a_2}{a_1+a_2}=\dfrac{2.3}{2+3}=1,2(m/s^2)\)