Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ hình:
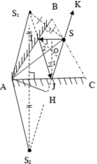
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...


a,Cách vẽ đường đi của tia sáng phát ra từ D, phản xạ lần lượt trên AB, AC rồi quay về S. Chứng tỏ rằng độ dài đường đi đó bằng SS2:
Gọi S1 là ảnh của S qua gương AB.
S2 là ảnh của S1 qua gương AC.Do đó S1 là đối xứng của S qua AB.
S2 là đối xứng của S qua AC (như hình 6). Ta tưởng tượng rằng ta đang nằm trên “chiếc giường” AC, mắt không nhìn vào điểm sáng S mà nhìn vào gương AB. Lúc đó ta thấy tia sáng không xuất phát từ S mà dường như xuất phát từ S1 đối xứng với S qua gương AB. Tương tự như vậy, nếu đặt mắt ở S không nhìn vào gương AB mà nhìn vào gương AC, ta sẽ thấy tia sáng không xuất phát từ S1mà dường như xuất phát từ S2 đối xứng với S1 qua gương AC. Từ đó suy ra cách vẽ các tia cần tìm.
b,
b,
Chứng tỏ đường đi của tia sáng trong câu a) không lớn hơn chu vi tam giác SMN.
Chọn M ∈ AB ; N ∈ AC.
Nối SM, MN, NS.
Ta phải so sánh chu vi tam giác SMN với chu vi tam giác SIJ. Hay ta so sánh chu vi tam giác SMN với chiều dài SS2.
Dễ thấy: SM = S1M => SM + MN = S1M + MN ≥ S1N.
Mà S1N= S2N => SM + MN ≥ S2N.
=> SM + MN + NS ≥ S2N + NS ≥ SS2
=> độ dài đường đi SS2 ≤ SM + MN + NS ≡ (chu vi ∆SMN) (đpcm)
Dấu “=” xảy ra khi và chỉ khi M ≡ I và N ≡ Jthui nha
Vậy ...
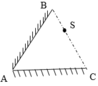
Hình tự vẽ!!!
lấy S1 đ/xug với S qua AB,S2 đối xứng với S qua AC.
-Nối S1S2 lần lượt cắt AB tại I cắt AC tại J.
-Nối SI,IJ,JS.
P/S:kí hiệu đường truyền tia sáng....