Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích của hình thoi là: 6 .8 : 2 = 24 cm^2
Cạnh của hình thoi là: \(\sqrt{\left(\frac{6}{2}\right)^2+\left(\frac{8}{2}\right)^2}=5\) cm
Chiều cao của hình thoi là: 24 : 5 = 4,8 cm
Vậy:...

a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)

Ta có hình thoi ABCD; 2đchéo AC;BD vuông góc và cắt nhau tai TĐ O của mỗi đường
Xét tam giác vuông AOB có:
AO= 1/2 . 9,6=4,8 cm
BO=1.2 . 7,2= 3,6 cm
áp dụng định lí py ta go trong tam giác trên ta được:
AO2+BO2=AB2
=>(4,8)2+(3,6)2 =AB2
=>AB2=36=62
=>AB=6 (vì AB>0)
mà AB+BC+CD+DA
=>chu vi ht = AB+BC+CD+DA=6.4=24cm

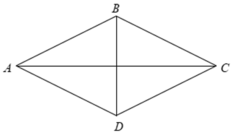
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :


Chu vi hình thoi là : 6.(8:2)= 24
tại sao ra nhu vậy