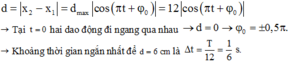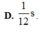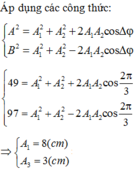Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Khoảng cách giữa hai vật theo phương Ox là:
![]()
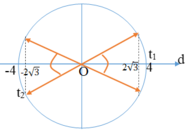
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

Chọn đáp án C
+ Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
+ Giả sử chọn t = 0 ⇒ x = x 0 = 10 3 c m nghĩa là t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
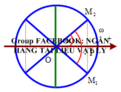
+ Theo hình vẽ ở tai thời điểm t1: 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t1
Từ M1 đến M2: t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t
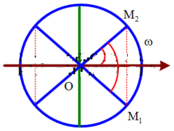

Chọn đáp án C
Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
Giả sử chọn φ = 0 nghĩa là t = 0 ⇒ x = x 0 = 10 3 c m
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
Theo hình vẽ ở tai thời điểm t 1 : 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t 1
Từ M 1 đ ế n M 2 : t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án B
+ Khoảng cách giữa hai dao động được biểu diễn bằng một hàm điều hòa