
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
Gọi \(x_3;x_4\) là các nghiệm của pt cần tìm, ta có:
\(\left\{{}\begin{matrix}x_3+x_4=2x_1-x_2^2+2x_2-x_1^2\\x_3x_4=\left(2x_1-x_2^2\right)\left(2x_2-x_1^2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2x_1^3-2x_2^3+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2.3-3^2+2.1=-1\\x_3x_4=4.1-2\left(3^3-3.1.3\right)+1^2=-31\end{matrix}\right.\)
Theo định lý Viet đảo, pt cần tìm có dạng:
\(x^2+x-31=0\)


\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)


Câu 2:
\(B=\left(\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right)\cdot\dfrac{x-1}{2x+2\sqrt{x}-\sqrt{x}-1}\)
\(=\left(\dfrac{\sqrt{x}+\sqrt{x}+3}{\left(\sqrt{x}-1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}+3}{2\sqrt{x}-1}\)
Để B<0 thì \(2\sqrt{x}-1< 0\)
=>\(2\sqrt{x}< 1\)
=>0<x<1/4


Bài 8:
a: Thay x=16 vào P, ta được:
\(P=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{\sqrt{2}+1+2}{\sqrt{2}+1-1}=\dfrac{3+\sqrt{2}}{\sqrt{2}}=3\sqrt{2}+2\)

1.
\(\Delta'=\left(m+1\right)^2-\left(m^2+3m-7\right)=-m+8\)
Phương trình đã cho vô nghiệm khi và chỉ khi \(\Delta'< 0\)
\(\Rightarrow-m+8< 0\)
\(\Rightarrow m>8\)
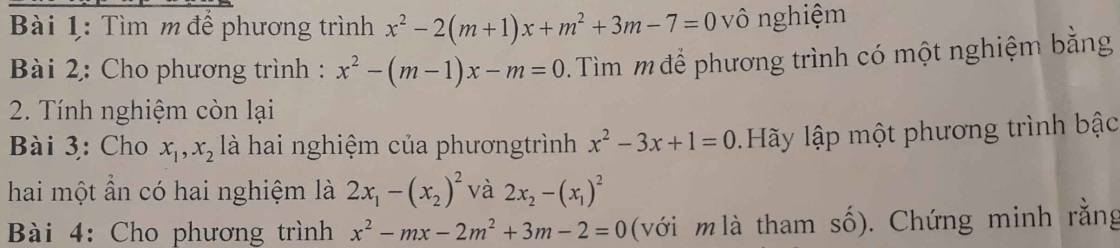

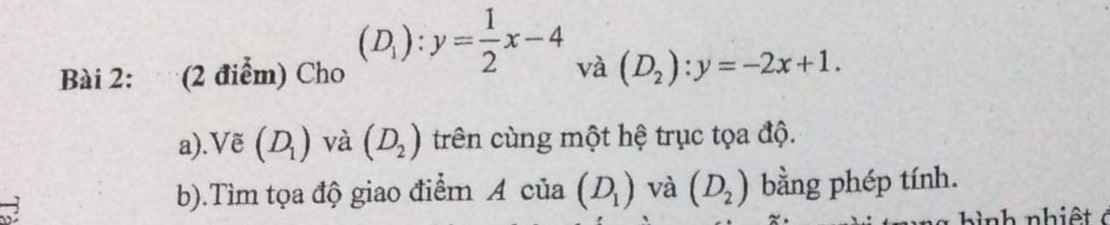
 câu 2 mn ơi mai mk phải hk r
câu 2 mn ơi mai mk phải hk r

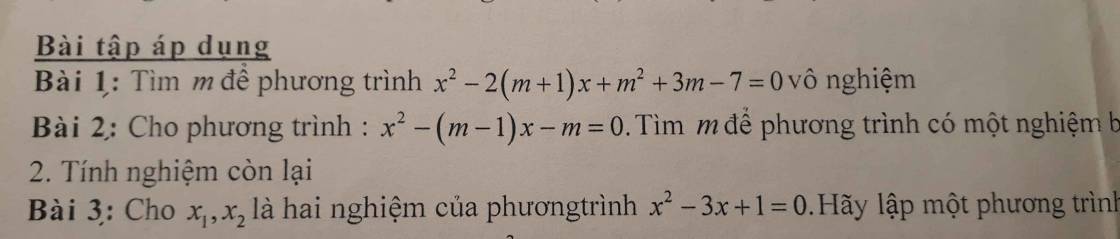
-.- ở đâu v
thi sớm vailoz
cho ké cái đề tham khảo :>