Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\sqrt{16x+m-4}=a\ge0\Rightarrow4-m=16x-a^2\)
Pt trở thành:
\(a=4x^2-18x+16x-a^2\Leftrightarrow4x^2-a^2-\left(2x+a\right)=0\)
\(\Leftrightarrow\left(2x-a\right)\left(2x+a\right)-\left(2x+a\right)=0\)
\(\Leftrightarrow\left(2x-a-1\right)\left(2x+a\right)=0\Rightarrow\left[{}\begin{matrix}2x-1=a\left(1\right)\\2x=-a\left(2\right)\end{matrix}\right.\)
Trước hết ta biện luận số nghiệm của (1) và (2) dựa vào m:
TH1: \(2x-1=a\Leftrightarrow\left\{{}\begin{matrix}x\ge\frac{1}{2}\\\left(2x-1\right)^2=16x+m-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\frac{1}{2}\\4x^2-20x+5=m\end{matrix}\right.\)
\(\Rightarrow\) \(m=-20\) pt có nghiệm duy nhất (nghiệm kép); \(-20< m\le-4\) pt có 2 nghiệm; \(m>-4\) pt có 1 nghiệm; \(m< -20\) vô nghiệm. (3)
TH2: \(-2x=a\Rightarrow\left\{{}\begin{matrix}x\le0\\4x^2=16x+m-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\le0\\4x^2-16x+4=m\end{matrix}\right.\)
\(\Rightarrow m< 4\) pt vô nghiệm; \(m\ge4\) pt có một nghiệm (4)
Từ (3);(4) ta có nhận xét:
- Nếu \(m\ge4\Rightarrow\) (1) và (2) đều có nghiệm duy nhất \(\Rightarrow\) phương trình đã cho có 2 nghiệm (loại)
- Nếu \(m< -20\) cả 2 pt đều vô nghiệm (loại)
- Nếu \(-20< m\le-4\) \(\Rightarrow\left(1\right)\) có 2 nghiệm, (2) vô nghiệm \(\Rightarrow\) pt có 2 nghiệm (loại)
- Nếu \(m=-20\) thì (1) có 2 nghiệm, (2) vô nghiệm (nhận)
- Nếu \(-4< m< 4\Rightarrow\) (1) có 1 nghiệm, (2) vô nghiệm \(\Rightarrow\) pt đã cho có 1 nghiệm (nhận)
Vậy \(\left[{}\begin{matrix}m=-20\\-4< m< 4\end{matrix}\right.\) thì tập nghiệm của pt có 1 phần tử
\(\Rightarrow\sum T=-20\) (khoảng \(\left(-4;4\right)\) các giá trị nguyên của m triệt tiêu khi cộng lại)

x − m x + 1 = x − 2 x − 1 ⇔ x ≠ ± 1 m x = m + 2
Phương trình đã cho có nghiệm ⇒ m ≠ 0 x = 1 + 2 m ≠ ± 1 ⇔ m ≠ 0 m ≠ 1
Vì m ∈ Z, m ∈ [−3; 5] nên m ∈ S = {−3; −2; 1; 2; 3; 4; 5}.
Đáp án cần chọn là: D

Phương trình viết lại m + 1 x = 3 m 2 - 1 x = 1 - m
Phương trình đã cho có nghiệm duy nhất khi 3 m 2 - m - 2 ≠ 0 ⇔ m ≠ 1 m ≠ − 2 3
Do m ∈ Z và m ∈ [−5; 10] ⇒ m ∈ {−5; −4; −3; −2; −1; 0; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Do đó, tổng các phần tử trong S bằng 39.
Đáp án cần chọn là: B

Phương trình có nghiệm khi ∆ = m 2 - 144 ≥ 0 ⇔ m 2 ≥ 12 2 ⇔ m ≥ 12 m ≤ − 12
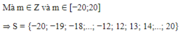
Do đó tổng các phần tử trong tập S bằng 0
Đáp án cần chọn là: D

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)