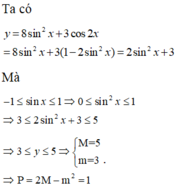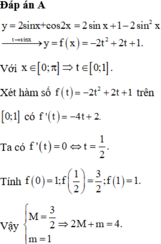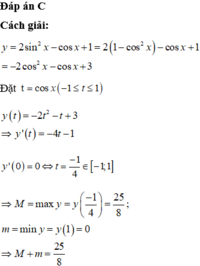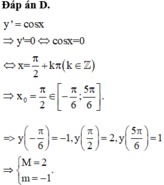Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Do $\cos x\in [-1;1]$ với mọi $x\in\mathbb{R}$ nên $\cos^2 x\in [0;1]$
$\Rightarrow 4-3.1\leq 4-3\cos ^2x\leq 4-3.0$
$\Rightarrow 1\leq y\leq 4$
$\Rightarrow M=4; m=1$
$\Rightarrow M+m=5$

\(M=2\cdot\left(1-cos^2x\right)-cosx+1\)
\(=-2\cdot cos^2x-cosx+1\)
\(=-2\cdot\left(cos^2x+\dfrac{1}{2}cosx-\dfrac{1}{2}\right)\)
\(=-2\cdot\left(cos^2x+2\cdot cosx\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{9}{16}\right)\)
\(=-2\cdot\left(cosx+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\)
-1<=cosx<=1
=>-3/4<=cosx+1/4<=5/4
=>0<=(cosx+1/4)^2<=25/16
=>0>=-2*cos(x+1/4)^2>=-25/8
=>9/8>=-2*cos(x+1/4)^2+9/8>=-25/8+9/8=-16/8=-2
=>M=9/8; m=-2
=>M+m=-7/8

\(y=1-2sin^22x+2sin^42x\)
\(y=2\left(sin^22x-\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)
\(y_{min}=\frac{1}{2}\) khi \(sin^22x=\frac{1}{2}\)
\(y=2sin^22x\left(sin^22x-1\right)+1\)
Do \(0\le sin^22x\le1\Rightarrow2sin^22x\left(sin^22x-1\right)\le0\)
\(\Rightarrow y\le1\Rightarrow y_{max}=1\) khi \(sin^22x=1\)