K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
??????????????
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
30 tháng 12 2021
\(\text{f(1)=}2.1^2+1=3\)
\(\text{f(-1)=}2.\left(-1\right)^2+1=3\)
\(\text{f(2)=}2.2^2+1=9\)
\(\text{f(0)=}2.0^2+1=1\)
\(\text{f(-3)=}=2.\left(-3\right)^2+1=19\)
6 tháng 10 2018
có sự nhầm lẫn gì đó thì phải hoặc ko
căn 31+ căn 17+ căn 3> 11
căn 31+ căn 7 +căn 3> 11
căn 31+ căn 17 +căn 3= căn 51 ko biến đổi được bỏ căn đi thì 51 >11
câu tiếp theo tương tự
17 tháng 10 2017
[2x + 1 ]\(^2\) = 1
[ 2x + 1 ]\(^2\) = 1\(^2\)
\(\Rightarrow\) 2x + 1 = 1
2x = 0
x = 0
Vậy : x = 0
TK
1
17 tháng 10 2021
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
15 tháng 5 2021
a) Xét ΔABM và ΔECM có
MC=MB(M là trung điểm của BC)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MA=ME(gt)
Do đó: ΔABM=ΔECM(c-g-c)
Suy ra: AB=EC(hai cạnh tương ứng)
TH
15 tháng 10 2021
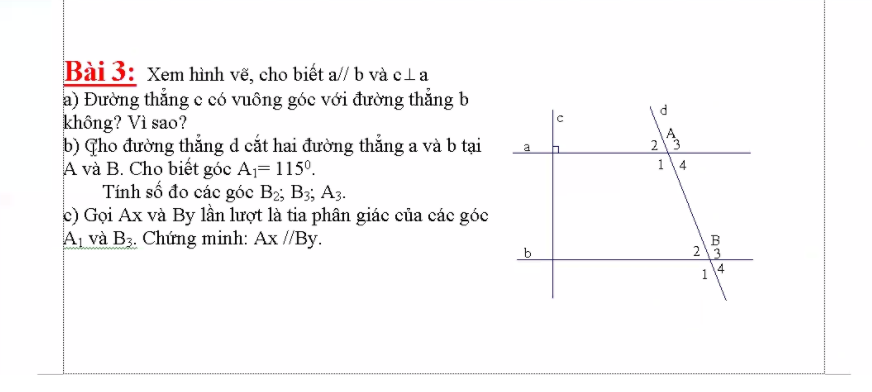
\(\)a//b
\(c\perp a\)
\(\Rightarrow c\perp b\)
\(\widehat{A1}=\widehat{A3}\) (đối đỉnh)
\(\widehat{A3}=\widehat{B3}\) (đồng vị)
\(\widehat{B3}+\widehat{B2}=180^o\) (kề bù)
\(\Rightarrow\widehat{B2}=180^o-115^o=65^o\)
TRẢ LỜI:
Gọi số học sinh các khối 6,7,8,9 lần lượt là x, y, z, t (học sinh)
Số học sinh bốn khối 6 , 7 , 8 , 9 tỉ lệ với các số 9 ; 8 ; 7 ; 6 nghĩa là :
Số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh nghĩa là y – t = 70.
Theo tính chất của dãy tỉ số bằng nhau ta có
Vậy số học sinh khối 6, 7, 8, 9 lần lượt là 315 ; 280 ; 245 ; 210 học sinh
cảm ơn bn