Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ps : Bn tự vẽ hình nhé, mk chỉ giải thôi ạ.
a) Xét \(\Delta ABC\)và \(\Delta HAB\)
\(\widehat{BAC}=\widehat{BHA}=90^O\)
\(\widehat{ABC}chung\)
\(\Rightarrow\Delta ABC~\Delta HBA\)( g - g )
b) Xét \(\Delta AHD\)và \(\Delta CED\)
\(\widehat{AHD}=\widehat{CED}=90^O\)
\(\widehat{ADH}=\widehat{CDE}\)( đối đỉnh )
\(\Rightarrow\Delta AHD~\Delta CED\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AD}=\frac{CE}{CD}\Rightarrow AH.CD=AD.CE\)
c) Vì H là trung điểm của BD mà \(AH\perp BD\)
=> AH là đường trung trực của BD
\(\Rightarrow AB=AD\)
Mà : \(\frac{AH}{AD}=\frac{CE}{CD}\)
\(\Rightarrow\frac{AH}{AB}=\frac{CE}{CD}\)
Vì \(\Delta ABC~\Delta HBA\Rightarrow\frac{AH}{AB}=\frac{CA}{CB}\)
Do đó : \(\frac{CE}{CD}=\frac{CA}{CB}=\frac{8}{10}=\frac{4}{5}\)
Vì \(\Delta CED\)vuông
\(\Rightarrow S_{CED}=\frac{CE.ED}{2}\)
\(AB//FK\Rightarrow\widehat{BAH}=\widehat{KFH}\)
\(\widehat{AHB}=\widehat{FHK}=90^O\)
\(BA=HD\)
\(\Rightarrow\Delta AHB=\Delta FHK\)
\(\Rightarrow HA=HF\)mà \(CH\perp AF\)
=> CH là đường trung trực AF \(\Rightarrow\Delta ACF\)cân tại C
Do đó : D là trọng tâm \(\Delta ACF\)
\(\Rightarrow CD=\frac{2}{3}CH\)
Mà \(\cos ACB=\frac{AC}{BC}=\frac{CH}{CA}=\frac{4}{5}\Rightarrow CH=\frac{32}{5}\Rightarrow CD=\frac{64}{15}\)
\(\Rightarrow\frac{CE}{CD}=\frac{4}{5}\Rightarrow CE=\frac{256}{75}\)
\(ED=\sqrt{CD^2-CE^2}=\frac{64}{25}\)
\(\Rightarrow S_{CED}=\frac{8192}{1875}\)
d) Vì \(\Delta ACF\)cân tại C \(\Rightarrow KE//AF\Rightarrow\widehat{EKF}=\widehat{AFK}\)
Vì HK là trung tuyến \(\Delta AFK\)\(\Rightarrow\widehat{AFK}=\widehat{HKF}\)
Do đó : \(\widehat{HKF}=\widehat{EKF}\)
=> KD là phân giác \(\widehat{HKE}\)
# Aeri #

Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
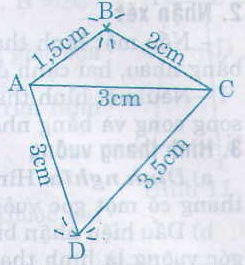
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.
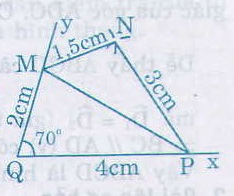
* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc ˆxOy=700xOy^=700
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.
Bài giải:
Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.

* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc ˆxOy=700xOy^=700
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.


dễ òm
ta lấy: 9-1=8 ; 9-1=8 =>119=88
5-1=4 ; 5-4=1 =>145=41
9-1=8;9-7=2 => 179=82
=>9-1=8 ; 9-6=3 => 169=83
cách làm