NT
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 5 2021
`1)((sqrt{14}-sqrt7)/(1-sqrt2)+(sqrt{15}-sqrt5)/(1-sqrt3)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt2-1))/(1-sqrt2)+(sqrt5(sqrt3-1))/(1-sqrt3):1/(sqrt7-sqrt5)`
`=(-sqrt7-sqrt5):1/(sqrt7-sqrt5)`
`=-(sqrt7+sqrt5).(sqrt7-sqrt5)`
`=-(7-5)`
`=-2`
`2)B=(2sqrtx-9)/(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)-(2sqrtx+1)/(3-sqrtx)`
`=(2sqrtx-9-x+9+2x-3sqrtx-2)/(x-5sqrtx+6)`
`=(x-sqrtx-2)/(x-5sqrtx+6)`
`=((sqrtx-2)(sqrtx+1))/((sqrtx-2)(sqrtx-3))`
`=(sqrtx+1)/(sqrtx-3)`
`x=11+6sqrt2`
`=(3+sqrt2)^2`
`=>B=(4+2sqrt2)/(sqrt2)`
`=2+2sqrt2`
25 tháng 5 2021
`3)5x^4+4x^2-1=0`
Đặt `t=x^2(t>=0)`
`pt<=>5t^2+4t-1=0`
`a-b+c=0`
`=>t_1=-1(l),t_2=1/5(tm)`
`<=>x=+-sqrt{1/5}`
Vậy `S={-sqrt{1/5},+sqrt{1/5}}`
P
1
17 tháng 1 2024
Bài I:
1: Thay x=4 vào A, ta được:
\(A=\dfrac{4}{2+1}=\dfrac{4}{3}\)
2: \(B=\dfrac{3}{\sqrt{x}+1}+\dfrac{x+5}{x-1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3}{\sqrt{x}+1}+\dfrac{\left(x+5\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)+x+5-\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3\sqrt{x}-3+x-\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
3: P=A*B
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{x}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}-1}\)
P<=4
=>P-4<=0
=>\(\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-1}< =0\)
=>\(\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}< =0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<=x<1
27 tháng 7 2021
Bài 1:
Phần a bạn tự làm nha! (Đ/S: 0,5)
b, B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}\) với \(x\ge0;x\ne4;x\ne9\)
B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{1}{\sqrt{x}-2}=\dfrac{\sqrt{x}+2}{x-4}\)
Vậy ...
c, Ta có: A = \(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\)= \(\dfrac{1}{\sqrt{x}+1}\)
T = \(\dfrac{A}{B}\)= \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)= 1 - \(\dfrac{3}{\sqrt{x}+1}\)
Ta có: x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}\ge0\) \(\Leftrightarrow\) \(\sqrt{x}+1\ge1\) \(\Leftrightarrow\) \(\dfrac{3}{\sqrt{x}+1}\le3\) \(\Leftrightarrow\) \(-\dfrac{3}{\sqrt{x}+1}\ge-3\) \(\Leftrightarrow\) T \(\ge\) -2
Vậy ...
Bài 2: ĐK: x \(\ge\) 0
Giả sử: \(P\) < \(\sqrt{P}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{x}+2}{\sqrt{x}+5}< \dfrac{\sqrt{\sqrt{x}+2}}{\sqrt{\sqrt{x}+5}}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)}{\sqrt{x}+5}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)>0\) (\(\sqrt{x}+5>0\) với mọi x \(\ge\) 0)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{\sqrt{x}+5-\sqrt{x}-2}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{3}>0\)
\(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}>0\)
Vì x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}+2\ge2\) \(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}\ge\sqrt{2}>0\) (Đpcm)
Vậy \(P\) < \(\sqrt{P}\)
Chúc bn học tốt!
PN
20 tháng 4 2022
DKXD : \(x\ge-1;y\ne-1\)
Dat : \(\left\{{}\begin{matrix}\sqrt{x+1}=a\left(a\ge0\right)\\y+1=b\left(b\ne0\right)\end{matrix}\right.\)
hpt<=>\(\left\{{}\begin{matrix}a+2-\dfrac{2}{y+1}=2\\2a-\dfrac{1}{y+1}=\dfrac{3}{2}\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}a+2-\dfrac{2}{b}=2\\2a-\dfrac{1}{b}=\dfrac{3}{2}\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}a-\dfrac{2}{b}=0\\4a-\dfrac{2}{b}=3\end{matrix}\right.< =>\left\{{}\begin{matrix}3a=3\\a=\dfrac{2}{b}\end{matrix}\right.< =>\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)(tmdk)
\(=>\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)(tmdk)
21 tháng 10 2021
c: Xét ΔBAC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BM\)
P
1
30 tháng 10 2021
\(2,\\ a,=6+12-15=3\\ b,=\left(2\sqrt{2}-3\sqrt{2}\right)\sqrt{2}=-\sqrt{2}\cdot\sqrt{2}=-2\\ c,=\dfrac{2\left(\sqrt{3}-1\right)}{2}-\dfrac{\sqrt{3}+2}{-1}+\dfrac{6\left(3-\sqrt{3}\right)}{6}\\ =\sqrt{3}-1+\sqrt{3}+2+3-\sqrt{3}=4+\sqrt{3}\)
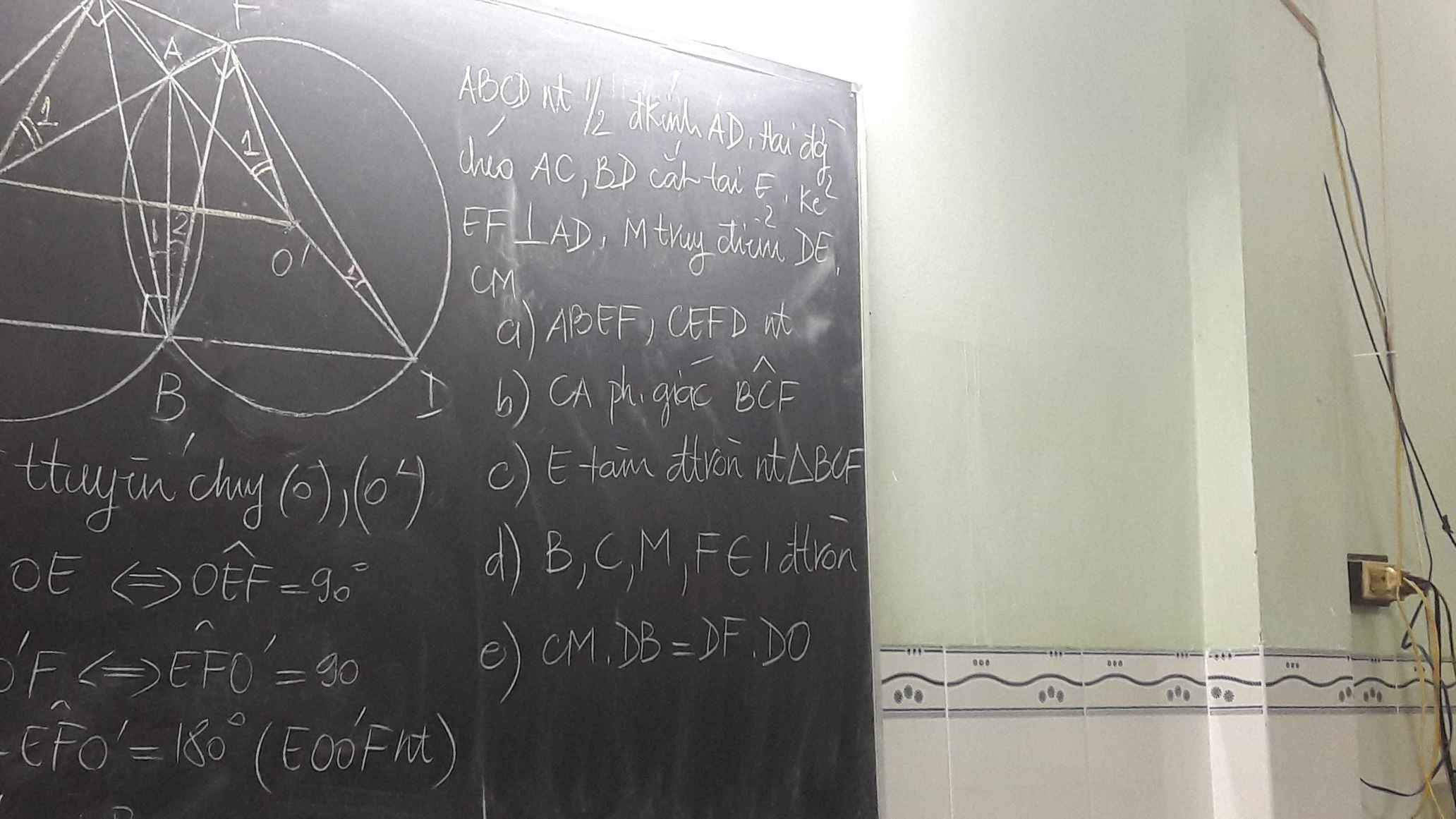
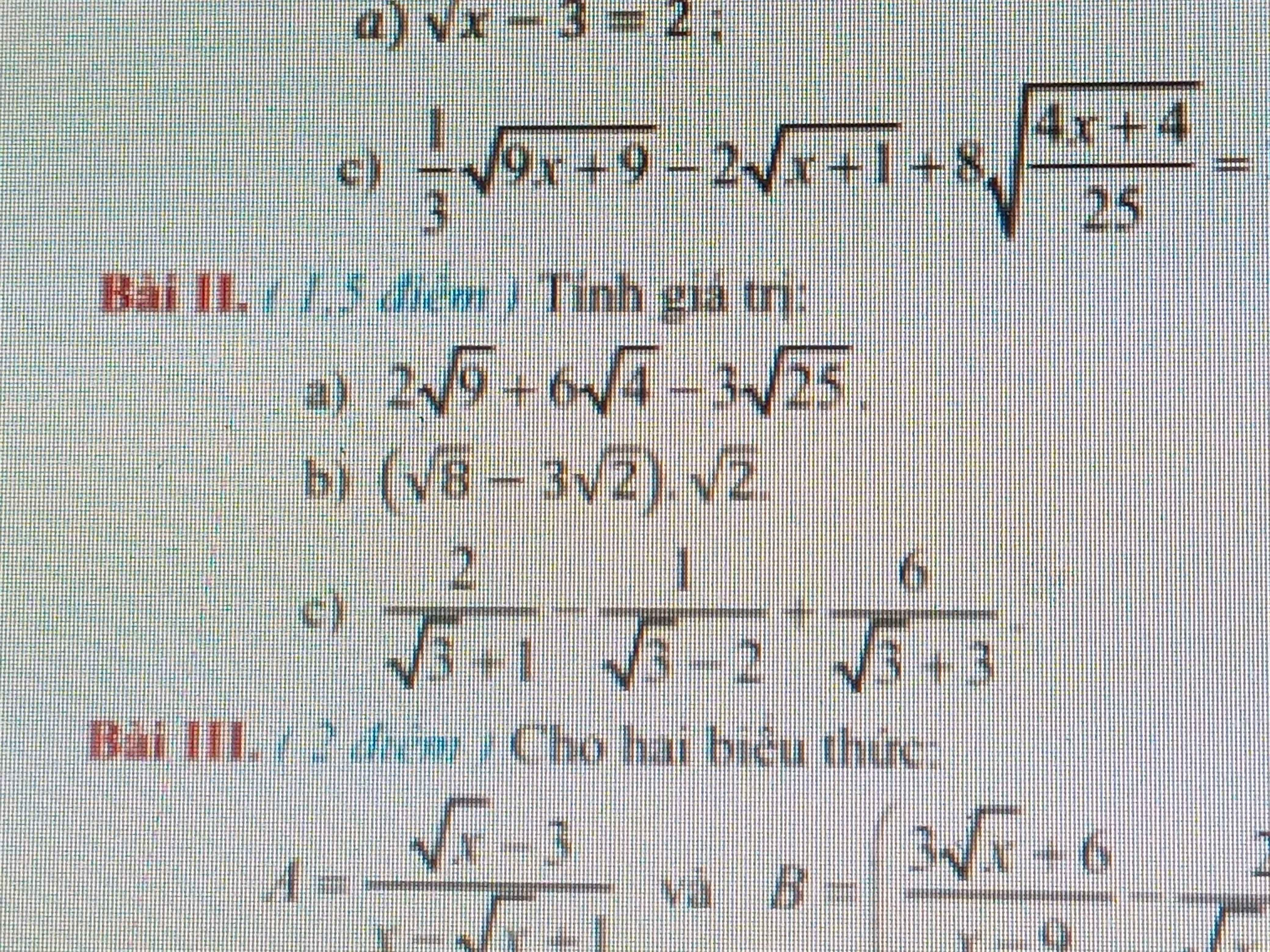
a, M thuộc đường tròn đk AB
=> AMB là góc nội tiếp chắn cung AB
=> ^AMB = 1/2 sđ cung AB
mà cung AB = 180 do AB là đường kính
=> ^AMB = 90
b, gọi I là trung điểm của AB
=> MI là đường trung tuyến của tam giác vuông AMB
=> MI = 1/2AB = IA = IB
=> M thuộc đường tròn đường kính AB
Bài 2 :
a, Gọi I là trung điểm HC
Xét tam giác HEC vuông tại E, I là trung điểm
\(IE=\frac{1}{2}HC=HI=IC\)(*)
Xét tam giác HDC vuông tại D, I là trung điểm
\(DI=\frac{1}{2}HC=HI=IC\)(**)
Từ (*) ; (**) suy ra D;H;E;C cùng thuộc đường tròn I đường kính HC
b, Gọi O là trung điểm AB
Xét tam giác ADB vuông tại D, O là trung điểm
\(OD=\frac{1}{2}AB=AO=BO\)(***)
Xét tam giác BEA vuông tại E, O là trung điểm
\(OE=\frac{1}{2}AB=AO=BO\)(****)
Từ (***) ; (****) suy ra A;E;D;B cùng thuộc đường tròn O, đường kính AB