Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

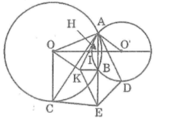
Gọi H là giao điểm của AB và OO’
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥ KB

A B O C H D E F K M I J
Gọi giao điểm của AK và MB là I; giao điểm của IF với AB là J.
Xét tam giác vuông ICA ta thấy DA = DC nên DA = DC = DI.
Lại có DB là trung trực của AF nên DA = DF. Vậy thì DA = DF = DI hay tam giác IFA vuông tại F, suy ra DB // IJ.
Vậy thì DB là đường trung bình tam giác AIJ hay B là trung điểm AJ.
Ta có KF // AJ nên áp dụng Ta let ta có:
\(\frac{KM}{AB}=\frac{IM}{IB}=\frac{MF}{BJ}\)
Do AB = BJ nên KM = MF.

Đường tròn c: Đường tròn qua B_1 với tâm O Đường tròn d: Đường tròn qua D_1 với tâm O' Đoạn thẳng k: Đoạn thẳng [O, K] Đoạn thẳng l: Đoạn thẳng [O', K] Đoạn thẳng m: Đoạn thẳng [C, A] Đoạn thẳng n: Đoạn thẳng [D, A] Đoạn thẳng p: Đoạn thẳng [O, A] Đoạn thẳng q: Đoạn thẳng [O', A] Đoạn thẳng r: Đoạn thẳng [A, B] Đoạn thẳng s: Đoạn thẳng [B, K] Đoạn thẳng t: Đoạn thẳng [O, O'] Đoạn thẳng g_1: Đoạn thẳng [J, O] Đoạn thẳng h_1: Đoạn thẳng [J', O'] Đoạn thẳng i_1: Đoạn thẳng [J, J'] O = (-0.72, 4.26) O = (-0.72, 4.26) O = (-0.72, 4.26) O' = (4.64, 4.02) O' = (4.64, 4.02) O' = (4.64, 4.02) Điểm A: Giao điểm đường của c, d Điểm A: Giao điểm đường của c, d Điểm A: Giao điểm đường của c, d Điểm B: Giao điểm đường của c, d Điểm B: Giao điểm đường của c, d Điểm B: Giao điểm đường của c, d Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm D: Giao điểm đường của d, g Điểm D: Giao điểm đường của d, g Điểm D: Giao điểm đường của d, g Điểm H: Giao điểm đường của f, h Điểm H: Giao điểm đường của f, h Điểm H: Giao điểm đường của f, h Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm K: Giao điểm đường của h, j Điểm K: Giao điểm đường của h, j Điểm K: Giao điểm đường của h, j Điểm J: Giao điểm đường của c, e Điểm J: Giao điểm đường của c, e Điểm J: Giao điểm đường của c, e Điểm J': Giao điểm đường của d, f_1 Điểm J': Giao điểm đường của d, f_1 Điểm J': Giao điểm đường của d, f_1
a) Ta thấy \(\widehat{OAH}+\widehat{HAI}=\widehat{OAI}=90^o\) và \(\widehat{O'AI}+\widehat{IAH}=\widehat{O'AH}=90^o\)
nên \(\widehat{OAH}=\widehat{O'AI}\Rightarrow\widehat{AOH}=\widehat{AO'I}\left(1\right)\)
Ta thấy \(\widehat{OAO'}+\widehat{HAI}=\widehat{OAH}+\widehat{HAI}+\widehat{IAO'}+\widehat{HAI}=\widehat{OAI}+\widehat{HAO'}\)
\(=90^o+90^o=180^o\)
Xét tứ giác AHKI ta cũng có \(\widehat{HKI}+\widehat{HAI}=180^o\Rightarrow\widehat{HKI}=\widehat{OAO'}\left(2\right)\)
Từ (1) và (2) suy ra tứ giác OAO'K là hình bình hành (Có các góc đối bằng nhau)
b) Gọi AJ và AJ' là hai đường kính của đường tròn (O) và (O')
Trước hết, ta có J, B, J' thẳng hàng. Thật vậy: \(\widehat{ABJ}+\widehat{ABJ'}=90^o+90^o=180^o\)
Ta chứng minh J, K ,J' cũng thẳng hàng.
Xét tam giác AJJ' có O' là trung điểm AJ', O'K // AJ, O'K = 1/2AJ
Vậy nên K là trung điểm JJ'.
Tóm lại J, B, K ,J' thẳng hàng.Vậy thì \(\widehat{ABK}=\widehat{ABJ'}=90^o\) hay \(KB\perp BA\)
Hình vẽ như trên
a) Ta thấy ^OAH+^HAI=^OAI=90o và ^O'AI+^IAH=^O'AH=90o
nên ^OAH=^O'AI⇒^AOH=^AO'I(1)
Ta thấy ^OAO'+^HAI=^OAH+^HAI+^IAO'+^HAI=^OAI+^HAO'
=90o+90o=180o
Xét tứ giác AHKI ta cũng có ^HKI+^HAI=180o⇒^HKI=^OAO'(2)
Từ (1) và (2) suy ra tứ giác OAO'K là hình bình hành (Có các góc đối bằng nhau)
b) Gọi AJ và AJ' là hai đường kính của đường tròn (O) và (O')
Trước hết, ta có J, B, J' thẳng hàng. Thật vậy: ^ABJ+^ABJ'=90o+90o=180o
Ta chứng minh J, K ,J' cũng thẳng hàng.
Xét tam giác AJJ' có O' là trung điểm AJ', O'K // AJ, O'K = 1/2AJ
Vậy nên K là trung điểm JJ'.
\(\Rightarrow\) J, B, K ,J' thẳng hàng.Vậy thì ^ABK=^ABJ'=90o hay KB⊥BA