VT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
6 tháng 8 2015
\(\frac{1}{2!}+\frac{2!}{4!}+...+\frac{198!}{200!}=\frac{1}{1.2}+\frac{1}{3.4}+...+\frac{1}{199.200}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-...+\frac{1}{199}-\frac{1}{200}=\left(\frac{1}{1}+\frac{1}{2}+...+\frac{1}{200}\right)-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{200}\right)\)
\(=\frac{1}{101}+\frac{1}{102}+...+\frac{1}{200}\)
11 tháng 11 2019
(n+2) chia hết (n+2)
=>[(3n+10)-(n+2)] chia hết cho (n+2)
[(3n+10)-(n+2)x3] chia hết cho (n+2)
[(3n+10)-(3n+6)] chia hết cho (n+2)
=4 chia hết cho (n+2)
Ư(4)={1;2;4}
| (n+2) | n | chọn/loại |
| 1 | -1 | loại |
| 2 | 0 | chọn |
| 4 | 2 | chọn |
n thuộc {0;2}
26 tháng 12 2021
pạn nào giải giúp mình bài này trước 16h đc ko ( mình năn nỉ đó )
D
28 tháng 10 2018
Ta có:
\(A=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}\)
\(\Rightarrow3A=1+\frac{2}{3}+\frac{3}{3^2}+\frac{4}{3^3}+...+\frac{100}{3^{99}}\)
\(\Rightarrow2A=1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\frac{1}{3^4}+...+\frac{1}{3^{99}}-\frac{100}{3^{100}}\)
\(\Rightarrow6A=3+1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\frac{1}{3^4}+...+\frac{1}{3^{98}}-\frac{100}{3^{99}}\)
\(\Rightarrow4A=3-\frac{101}{3^{99}}+\frac{100}{3^{100}}=3-\frac{203}{3^{100}}\)
\(\Rightarrow A=\frac{3-\frac{203}{3^{100}}}{4}=\frac{3}{4}-\frac{203}{3^{100}.4}< \frac{3}{4}\Rightarrowđpcm\)
Vậy \(A< \frac{3}{4}\)
KM
4
KV
14 tháng 10 2023
P = (10.10².10³.10⁴...10⁹) : (10⁵.10¹⁰.10²⁵)
= 10¹⁺²⁺³⁺⁴⁺⁵⁺⁶⁺⁷⁺⁸⁺⁹ 10⁵⁺¹⁰⁺²⁵
= 10⁴⁵ : 10⁴⁰
= 10⁴⁵⁻⁴⁰
= 10⁵
= 100000
14 tháng 10 2023
\(P=\left(10.10^2.10^3.10^4.....10^9\right):\left(10^5.10^{10}.10^{25}\right)\)
\(P=10^{45}:10^{40}\)
\(P=10^5\)
22 tháng 1 2024
Bài 5:
a: AC+CB=AB
mà A,B,C thẳng hàng
nên C nằm giữa A và B
b: AB+BC=AC
mà A,B,C thẳng hàng
nên B nằm giữa A và C
c: BA+AC=BC
mà B,A,C thẳng hàng
nên A nằm giữa B và C
Bài 6:
a: MN+NP=MP
mà M,N,P thẳng hàng
nên N nằm giữa M và P
b: MP+PN=MN
mà M,P,N thẳng hàng
nên P nằm giữa M và N
c: PN+NM=PM
mà P,N,M thẳng hàng
nên N nằm giữa P và M
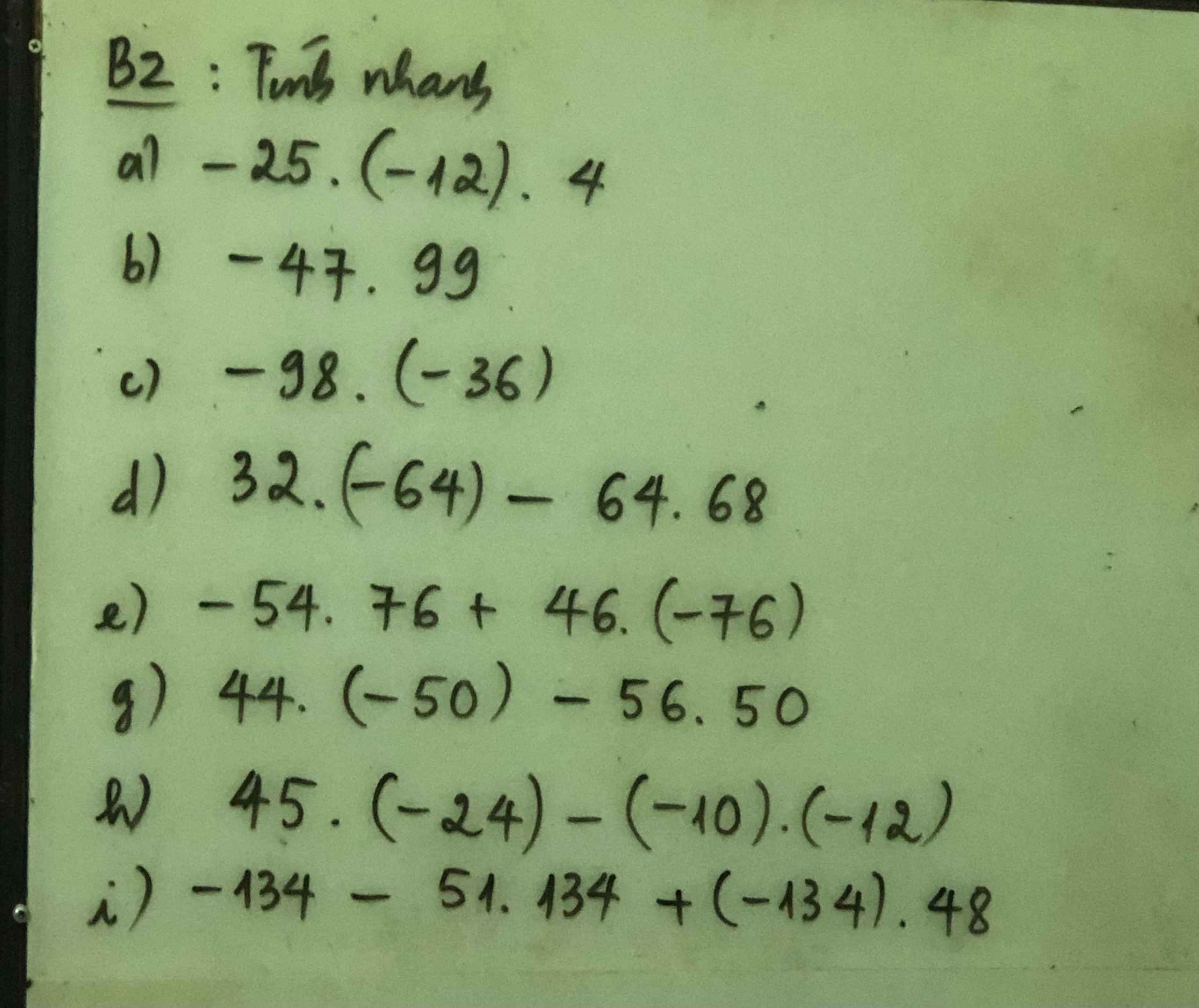
Bài 2 đâu hả bn
@Mina
#hoangphuong
gửi ảnh
ko báo cáo h