K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
2
TT
0
NH
1
13 tháng 7 2016
Tỉ số \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\) có thể rút gọn thành \(\frac{6}{5}\).Thử lại: \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\)=\(\frac{31}{\frac{5}{\frac{31}{6}}}\)=\(\frac{31}{5}\).\(\frac{6}{31}\)=\(\frac{6}{5}\)
ta có thể viết tỉ số khác cũng có thể "rút gọn" như vậy:VD: \(1\frac{7}{\frac{9}{2\frac{1}{7}}}\)=\(\frac{7}{8}\)
TN
1
2 tháng 10 2015
a) Xem hình vẽ.
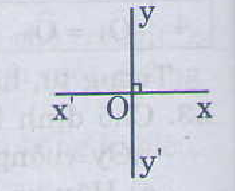
b)
c) Điền vào chỗ trống:
1) (vì là hai góc kề bù).
2) (theo giả thiết và căn cứ vào 1).
3) (căn cứ vào 2).
4) (vì là hai góc đối đỉnh).
5) (căn cứ vào 4 và giả thiết).
6) (vì là hai góc đối đỉnh).
7) (căn cứ vào 6 và 3).
d)Trình bày lại cách chứng minh một cách gọn hơn.
Ta có: (hai góc kề bù) mà
(gt)
nên .
Suy ra
Lại có (hai góc đối đỉnh).
Suy ra .
SW
1
SN
15 tháng 10 2021
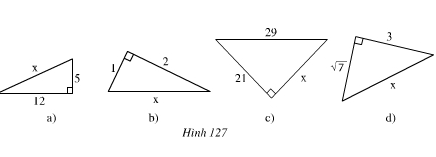
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
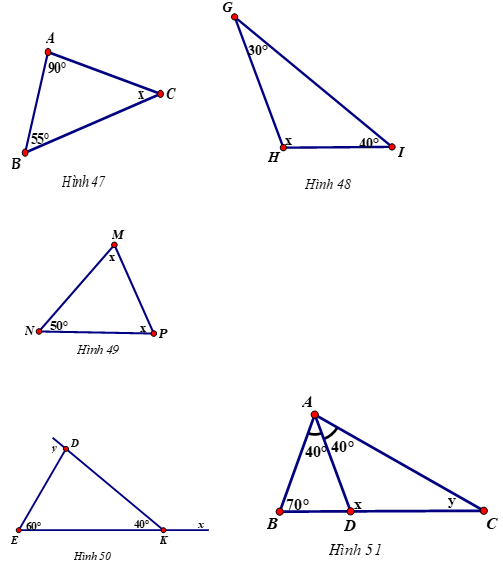
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.
NN
9
14 tháng 10 2021
TL
a) Ta có ˆBIKBIK^ là góc ngoài tại đỉnh II của ΔBAIΔBAI.
Nên ˆBIK=ˆBAI+ˆABI>ˆBAIBIK^=BAI^+ABI^>BAI^
Mà ˆBAK=ˆBAIBAK^=BAI^
Vậy ˆBIK>ˆBAKBIK^>BAK^ (1)
b) Ta có ˆCIKCIK^ là góc ngoài tại đỉnh II của ΔAICΔAIC
nên ˆCIK=ˆCAI+ˆICA>ˆCAICIK^=CAI^+ICA^>CAI^
Hay ˆCIK>ˆCAICIK^>CAI^ (2)
Từ (1) và (2) ta có:
ˆBIK+ˆCIK>ˆBAK+ˆCAIBIK^+CIK^>BAK^+CAI^
⇒ˆBIC>ˆBAC⇒BIC^>BAC^.
Hok tốt nha bn
#Kirito
NA
1
20 tháng 9 2017
a) 2n = 16/2=8= 23 => n =3
b) (-3)n = (-27).81 =(-3)3.34= (-3)7 => n = 7
c) 4 =22= 23n.2n = 23n-n = 22n => n =1
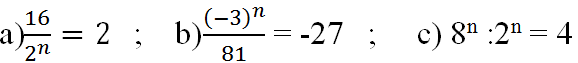
\(5\frac{1}{7}\)trên \(7\frac{1}{5}\)=\(\frac{5}{7}\)