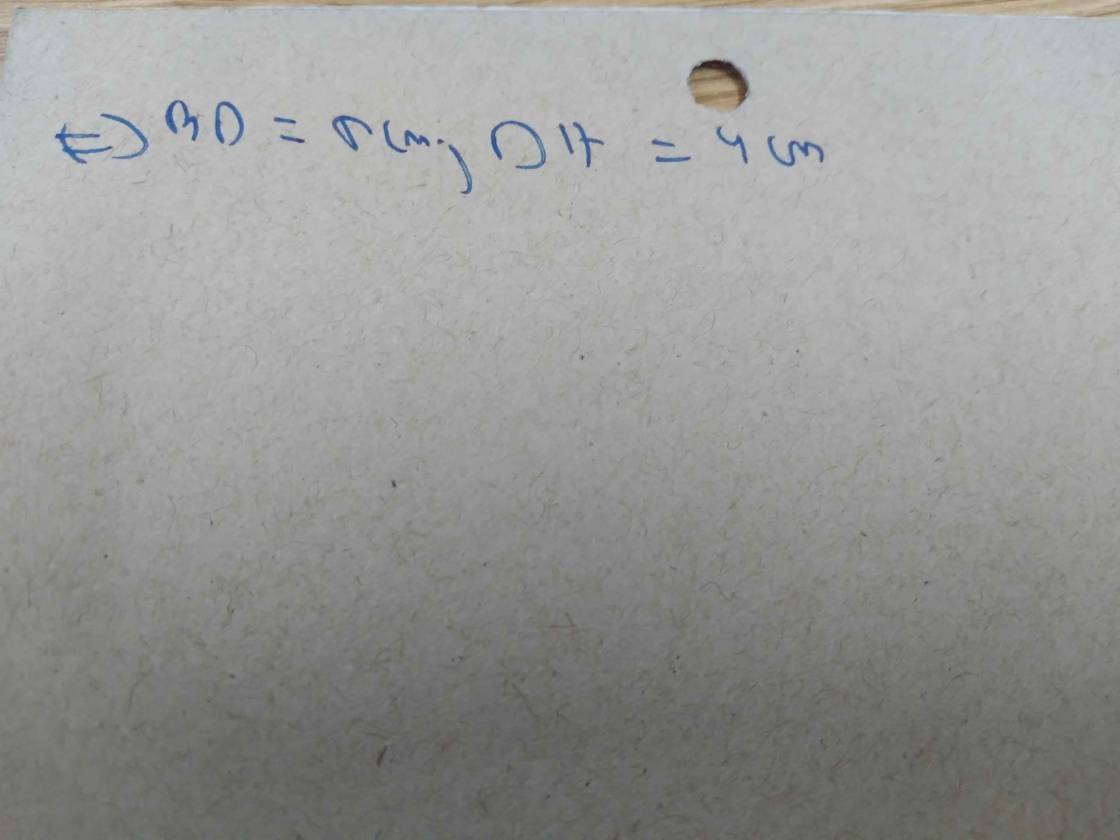Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
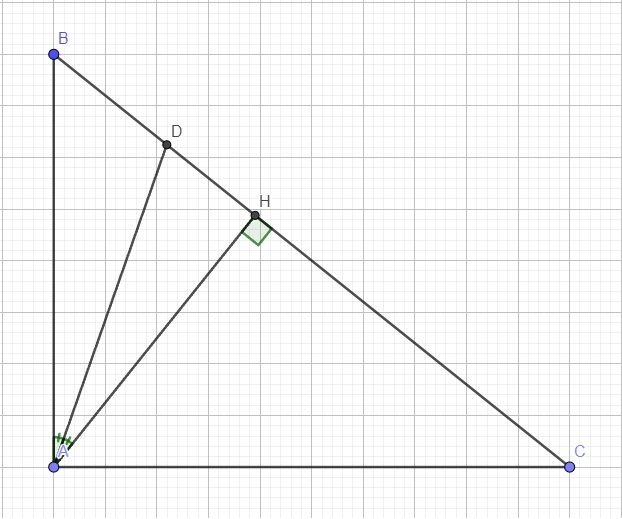
Xét hai tam giác HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BHA}=\widehat{BAC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Từ câu a ta có: \(\dfrac{HA}{AC}=\dfrac{BA}{BC}\Rightarrow HA=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
c.
Áp dụng định lý Pitago cho tam giác vuông HBA:
\(BH=\sqrt{AB^2-HA^2}=9\left(cm\right)\)
Do AD là phân giác, áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DH}{AH}\Rightarrow\dfrac{BD}{AB}=\dfrac{BH-BD}{AH}\)
\(\Rightarrow12BD=15\left(9-BD\right)\Rightarrow BD=5\left(cm\right)\)
\(\Rightarrow DH=BH-BD=4\left(cm\right)\)

A;áp dụng pitago ta có : BC2 = 202+152=625
suy ra : BC= \(\sqrt{625}\) =25
Xét tam giác :\(\Delta abc\)và \(\Delta ahc\)ta có :
\(\widehat{c}\) ( góc chung)
\(\widehat{ahc}\)= \(\widehat{bac}\) = 90 độ
vậy \(\Delta ABC\)đồng dạng với \(\Delta AHC\)( g-g)
suy ra : \(\frac{15}{25}\)= \(\frac{AH}{20}\)
vậy AH= 12 cm \(\left(ĐPCM\right)\)
B) ta có :áp dụng pitago ta có: BH^2 = 15^2-12^2=81 cm
vậy BH =\(\sqrt{81}\)=\(9\)cm
áp dụng đường phân giác trong tam giác ta lại có
\(\frac{DH}{DB}\)= \(\frac{15}{12}\)
\(_{_{ }\Leftrightarrow}\)\(\frac{9-DB}{DB}\) = \(\frac{15}{12}\)
\(\Leftrightarrow\) \(\left(9-DB\right)\)\(_{\times}\) \(12\)= \(15\times DB\)
\(\Leftrightarrow\) 108 -12DB=15DB
\(\Leftrightarrow\) 108 = 15DB+12DB
\(\Rightarrow\)DB=4 cm \(\left(ĐPCM\right)\)
DH= BH - BD= 9 - 4=5 \(\left(ĐPCM\right)\)
phần C mình gửi sau nhé bạn xin lỗi nhé ^_^
\(GIẢI\)\(TIEP\)
ta có : \(\widehat{HCF}\)= \(\widehat{CHA}\) =\(90\)độ ( giả thiết)
mà hai góc này lại ở vị trí sole trong suy ra :HA song song với CF
suy ra: \(\widehat{CFH}\)= \(\widehat{AHF}\) ( HAI GÓC SOLE TRONG )
\(\widehat{FCA}\) =\(\widehat{HAC}\)( HAI GÓC SOLE TRONG )
TỪ hai điều trên suy ra : \(\widehat{CMF}\)= \(\widehat{HMA}\)
mà hai góc này lại ở vị trí đối đỉnh của CA và HF suy ra:
HMF thẳng hàng

Đọc câu cuối thì chắc là chứng minh phản chứng đêý ạ ( Ngu lí thuyết, chắc thế.)
Đại khái cái cách này là bạn gọi 1 trong 3,4 điểm cần cm thẳng hàng ý trùng 1 điểm bâts kì thuộc (hoặc chứng minh được) thuộc đoạn thẳng có 2 mút là 2 điểm cần chứng minh ấy. Rồi từ dữ kiện đề bài => 2 điểm trùng nhau => thẳng hàng. Cơ bản mình hiểu là vậyyy ..
sao FC lại song song me do cùng vuông góc hc được .CF vuông góc với tia phân giác góc MEC mà chỉ

a. Xét tam giác HAC và tam giác ABC, có:
\(\widehat{C}\) : chung
\(\widehat{AHC}=\widehat{BAC}=90^o\)
Vậy tam giác \(HAC\sim\) tam giác \(ABC\) ( g.g )
b.\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\) (1)
Áp dụng định lý pytago tam giác ABC, ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\left(1\right)\Leftrightarrow AH=\dfrac{AC.AB}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)
c. Tam giác AHB có phân giác AD:
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{HD}{BD}\) (2)
(1)(2) \(\Rightarrow\dfrac{HD}{BD}=\dfrac{AC}{BC}\) hay \(\dfrac{BD}{HD}=\dfrac{BC}{AC}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm