
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đặt M là n^3 -9n^2+2n.
TH1 : n có dạng 2k => M chia hết cho 2 (bạn tự cm)
TH2 ; n có dạng 2k+1 => M = (2k+1)^3-9(2k+1)^2+2n
=8k^3+6k+12k^2+1-9(4k^2+4k+1)+2n = ... => M chia hết cho 2 với mọi n (1)
Xét n có dạng 3k => M chia hết cho 3
Xét n có dạng 3k+1 => n^3+2n=(3k+1)^3+2(3k+1)=27k^3+9k+27k^2+6k+3 chia hết cho 3 mà 9n^2 cũng chia hết cho 3 => M chia hết cho 3
Tương tự bạn xét n =3k+2....
=> M chia hết cho 3 vs mọi n (2)
Từ (1) và (2) => M chia hết cho 6

Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x-3\right)^2}\)
\(\Leftrightarrow2x-1=x-3\)
\(\Leftrightarrow2x-x=-3+1\)
\(\Leftrightarrow x=-2\)
Vậy phương trình có nghiệm x=-2
\(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x-3\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=x-3\\2x-1=3-x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=\frac{4}{3}\end{cases}}\)

Bài 4:
a: =>3x=24
hay x=8
b: =>5x-2x=-11+3
=>3x=-8
hay x=-8/3
c: =>4/3x=17
hay x=51/4
d: =>3/7x=-8
hay x=-56/3

1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)

:v a giúp e nè :P
\(x^5-x=2000\)
\(\Leftrightarrow x.\left(x^4-1\right)=2000\)
\(\Leftrightarrow x.\left(x^2-1\right).\left(x^2+1\right)=2000\)
\(\Leftrightarrow x.\left(x-1\right).\left(x+1\right).\left(x^2+1\right)=2000\)
vì VP chia hết cho 3 mà 2000 ko chia hết cho 3
Vậy....

a)=\(3x^3-15x^2+21x\)
b)\(=-2x^4y-10x^2y+2xy\)
c)\(=-x^3+6x^2+5x-4x^2+24x+20=-x^3+2x^2+29x+20\)
d)\(=2x^4-3x^3+4x^2-2x^2+3x-4=2x^4-3x^32x^2+3x-4\)
e)\(=x^2-4y^2\)
f)\(=-2x^2y^3+y-3\)
g)\(=3xy^4-\dfrac{1}{2}y^2+2x^2y\)
h)\(=9x^2-6x+1-7x^2-14=2x^2-6x-13\)
i)\(=x^2-x-3\)
j)\(=\left(x+2y\right)\left(x^2-2y+4y^2\right):\left(x+2y\right)=x^2-2y+4y^2\)

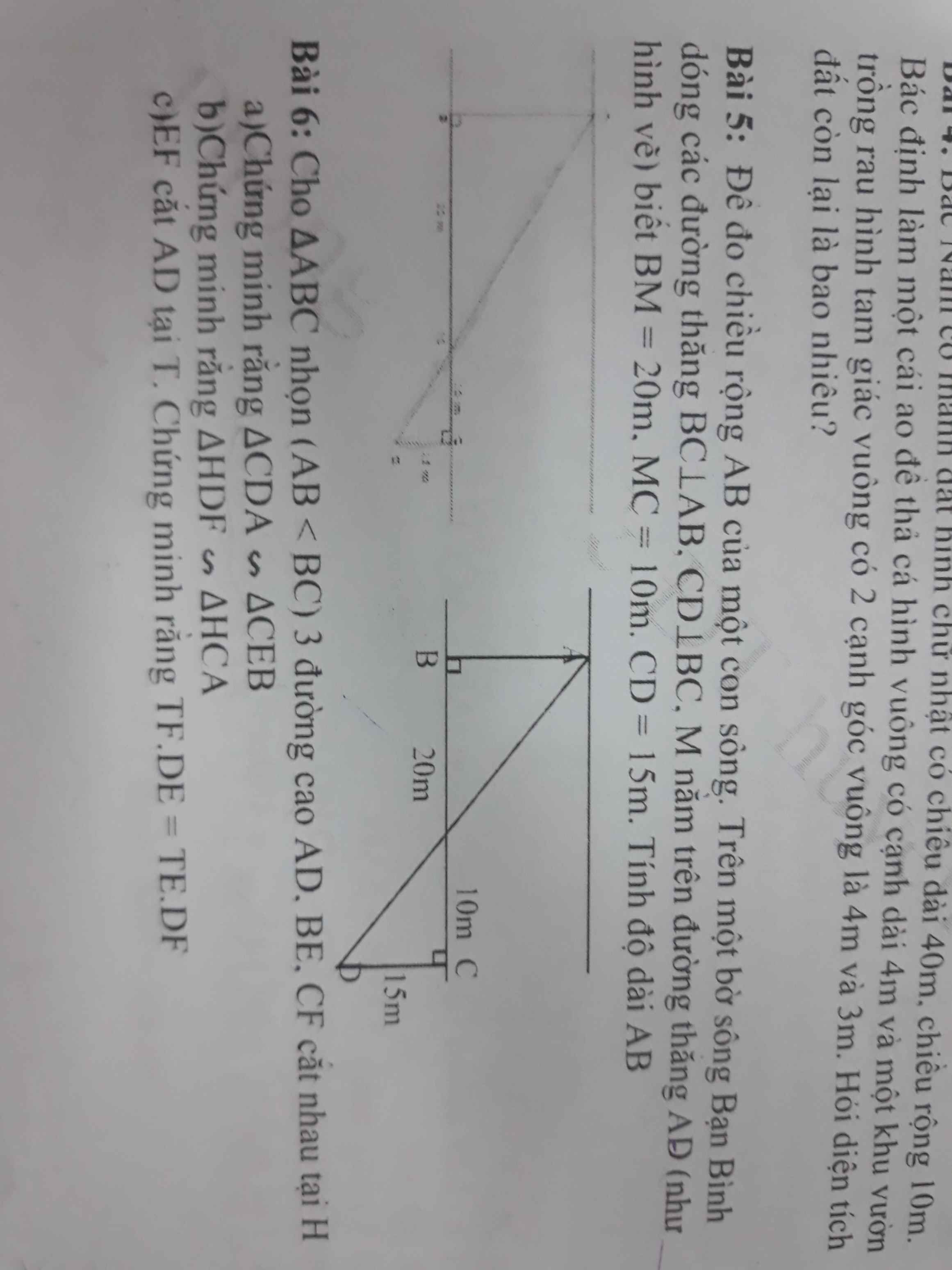
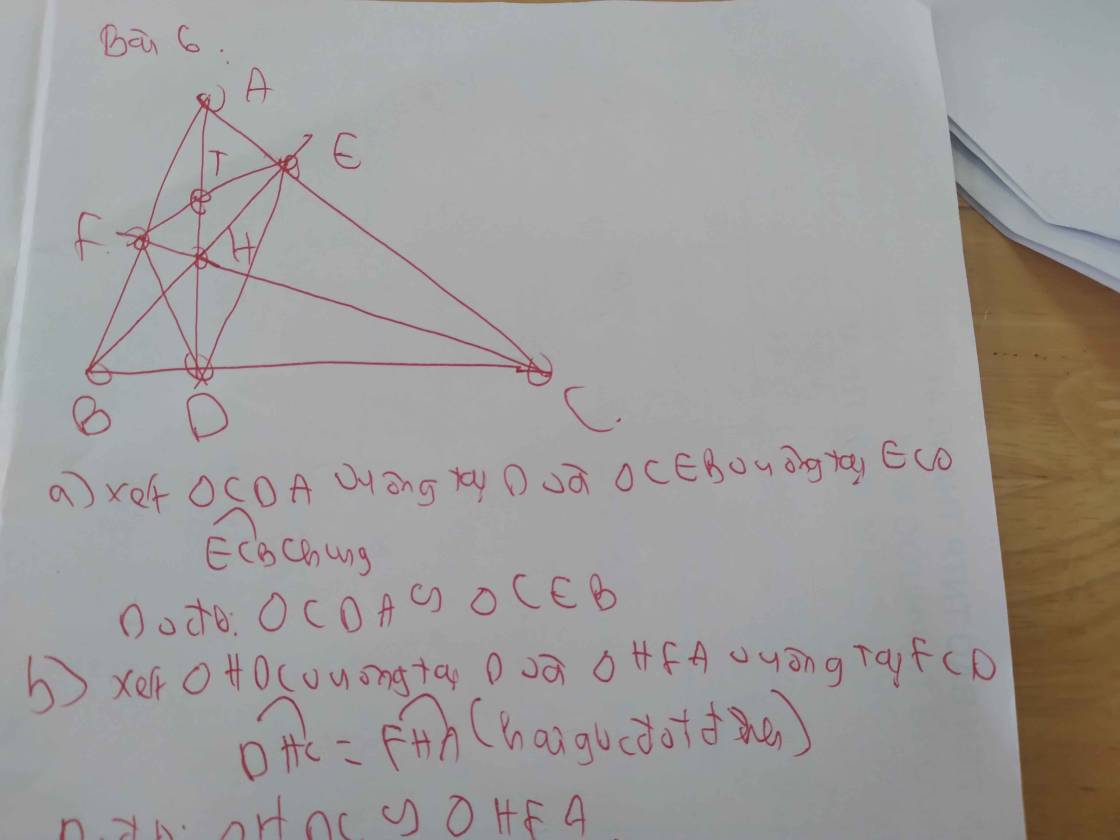


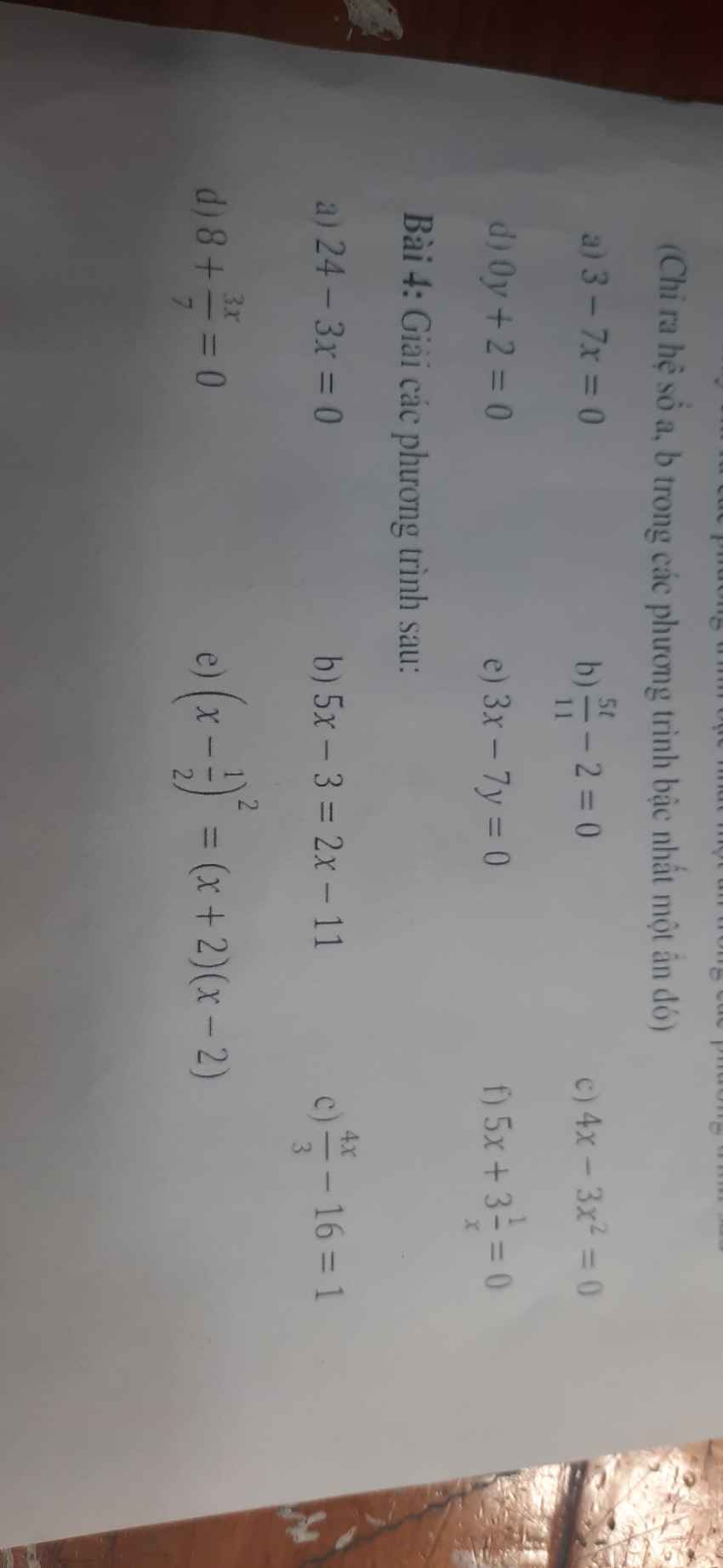
 lm hộ em vs ạ
lm hộ em vs ạ
Answer:
Bài 6:
\(M=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2+4x}{x^2-4}\left(x\ne\pm2\right)\)
\(=\frac{x+2-\left(x-2\right)+x^2+4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2-x+2+x^2+4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2}{x-2}\)
\(M=\frac{x+2}{x-2}=\frac{x-2+4}{x-2}=1+\frac{4}{x-2}\)
\(M\inℤ\Leftrightarrow x-2\inƯ\left(4\right)=\left\{\pm4;\pm2;\pm1\right\}\)
\(\Rightarrow x\in\left\{-2;0;1;3;4;6\right\}\) mà \(x\ne\pm2\)
Vậy \(x\in\left\{0;1;3;4;6\right\}\)
Bài 7:
Điều kiện của \(x\) để biểu thức \(A\) xác định
\(\hept{\begin{cases}3x+2x\ne0\\3x-2x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x\ne-3\\2x\ne3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne-\frac{3}{2}\\x\ne\frac{3}{2}\end{cases}}\)