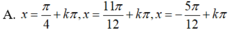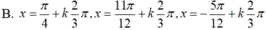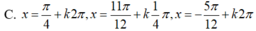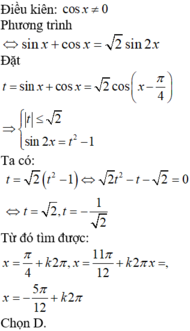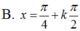K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
Đề là: \(2sin^22x-3cos2x+6sin^2x-9=0\) đúng không nhỉ?
\(\Leftrightarrow2\left(1-cos^22x\right)-3cos2x+3\left(1-cos2x\right)-9=0\)
\(\Leftrightarrow-2cos^22x-6cos2x-4=0\)
\(\Leftrightarrow cos^22x+3cos2x+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow...\)
CM
26 tháng 5 2018
Hướng dẫn giải
Chọn B.
Ta có: 4sin4 + 12cos2 x – 7 =0
ó 4sin4x – 12sin2 x + 5= 0
30 tháng 7 2019
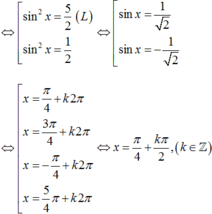
đúng y như trong đề luôn mà bạn , hay là bạn có tính sai chỗ nào đó rồi không
TV
0
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 12 2018
\(2cosx+3sinx+\dfrac{1}{3}cos2x-sin2x=\dfrac{8}{3}\)
\(\Leftrightarrow6cosx+9sinx+cos2x-3sin2x-8=0\)
\(\Leftrightarrow6cosx-6sinx.cosx+9sinx-9+1+1-2sin^2x=0\)
\(\Leftrightarrow6cosx\left(1-sinx\right)-9\left(1-sinx\right)+2\left(1-sinx\right)\left(1+sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx-9+2+2sinx=0\right)\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx+2sinx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}1-sinx=0\\6cosx+2sinx=7\end{matrix}\right.\)
TH1: \(1-sinx=0\Rightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
TH2: \(6cosx+2sinx=7\) (1)
Do \(6^2+2^2=40< 7^2=49\Rightarrow\) pt (1) vô nghiệm
Vậy pt đã cho có nghiệm \(x=\dfrac{\pi}{2}+k2\pi\)