NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 9 2022
a: \(\Leftrightarrow\dfrac{x\left(x^2-1\right)+x-1}{\left(x+1\right)\left(x-1\right)}=\dfrac{\left(2x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
=>\(x^3-x+x-1=2x^2+x-1\)
=>x^3-2x^2-x=0
=>x(x^2-2x-1)=0
=>x=0 hoặc \(x\in\left\{1+\sqrt{2};1-\sqrt{2}\right\}\)
c: =>(x-1)(x-2) căn 2x-3=0
=>\(x\in\left\{\dfrac{3}{2};2\right\}\)
giúp mình với nha mọi người
TA
28 tháng 12 2018
Bài 1 : Đồ thị đi qua điểm M(4;-3) \(\Rightarrow\) y=-3 x=4. Ta được:
\(-3=4a+b\)
Đồ thị song song với đường d \(\Rightarrow\) \(a=a'=-\dfrac{2}{3}\) Ta được:
\(-3=4.-\dfrac{2}{3}+b\) \(\Rightarrow\) \(b=-\dfrac{1}{3}\)
Vậy: \(a=-\dfrac{2}{3};b=-\dfrac{1}{3}\)
b) (P) đi qua 3 điểm A B O, thay tất cả vào (P), ta được hpt:
\(\hept{\begin{cases}a+b+c=1\\a-b-c=-3\\0+0+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=-1\\b=2\\c=0\end{cases}}}\)
Bài 2 : Mình ko biết vẽ trên này, bạn theo hướng dẫn rồi tự làm nhé
Đồ thị có \(a< 0\) \(\Rightarrow\) Hàm số nghịch biến trên R
\(\Rightarrow\) Đồ thị có đỉnh \(I\left(1;4\right)\)
Chọn các điểm:
x 1 3 -1 2 -2
y 4 0 0 3 -5
H
24 tháng 6 2019
1,\(pt\Leftrightarrow11x^2-5x+6=x^3+5x^2+6x\)
\(\Leftrightarrow x^3-6x^2+11x-6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\\x=1\end{matrix}\right.\)(tm)
P
3 tháng 12 2018
b)\(\Leftrightarrow\left\{{}\begin{matrix}x-4\ge0\\\sqrt{x^2-3x+8}=x-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\x^2-3x+8=\left(x-4\right)^2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\x^2-3x+8=x^2-8x+16\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\5x=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge4\\x=\dfrac{8}{5}\left(loại\right)\end{matrix}\right.\)=> pt vô nghiệm
c)\(\left\{{}\begin{matrix}8-x\ge0\\x^2-5x-2=\left(8-x\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x^2-5x-2=x^2-16x+64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le8\\11x=66\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x=6\left(nhận\right)\end{matrix}\right.\)
2 tháng 4 2017
\(a,\Leftrightarrow\dfrac{\left(3x+4\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}=\dfrac{4+3x^2-12}{\left(x-2\right)\left(x+2\right)}\)
ĐKXĐ:\(x\ne2;x\ne-2\)
\(\Rightarrow3x^2+10x+8-x+2-4-3x^2+12=0\)
\(\Leftrightarrow\)\(9x+18=0\)
\(\Leftrightarrow x=-2\)(loại).
Vậy phương trình vô nghiệm.
b,ĐKXĐ:\(x\ne\dfrac{1}{2}\)
PT đã cho \(\Rightarrow6x^2-4x+6-6x^2+13x-5=0\)
\(\Leftrightarrow9x+1=0\)
\(\Leftrightarrow x=-\dfrac{1}{9}\left(tmđk\right)\)
c,\(ĐKXĐ:x\ge2\)
Bình phương 2 vế ta được:
\(x^2-4-x^2+2x-1=0\)
\(\Leftrightarrow2x-5=0\)
\(\Leftrightarrow x=\dfrac{5}{2}\left(tmđk\right)\)
7 tháng 4 2017
lời giải
a) \(\left\{{}\begin{matrix}-2x+\dfrac{3}{5}>\dfrac{2x-7}{3}\left(1\right)\\x-\dfrac{1}{2}< \dfrac{5\left(3x-1\right)}{2}\left(2\right)\end{matrix}\right.\)
(1)\(\Leftrightarrow\)
\(\dfrac{3}{5}+\dfrac{7}{3}>\left(\dfrac{2}{3}+2\right)x\)
\(\dfrac{44}{15}>\dfrac{8}{3}x\) \(\Rightarrow x< \dfrac{44.3}{15.8}=\dfrac{11}{5.2}=\dfrac{11}{10}\)
Nghiêm BPT(1) là \(x< \dfrac{11}{10}\)
(2) \(\Leftrightarrow2x-1< 15x-5\Rightarrow13x>4\Rightarrow x>\dfrac{4}{13}\)
Ta có: \(\dfrac{4}{13}< \dfrac{11}{10}\) => Nghiệm hệ (a) là \(\dfrac{4}{13}< x< \dfrac{11}{10}\)
NN
0
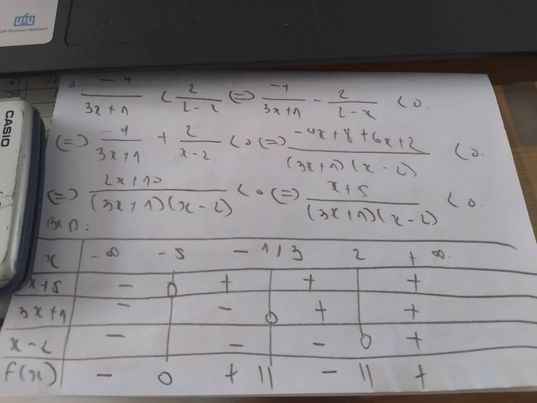
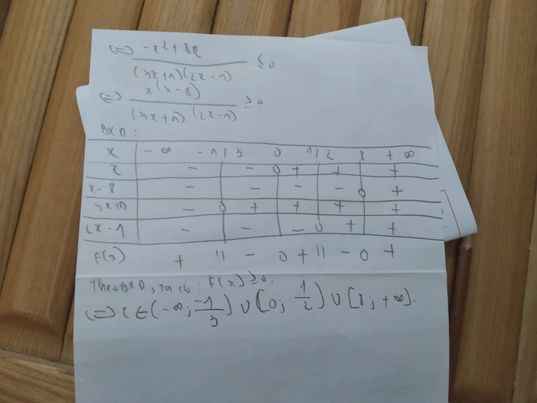
TH1: x>-2
Pt sẽ là \(\dfrac{x}{2x-1}=\dfrac{-3x-2}{x+2}\)
=>-6x^2+3x-4x+2=x^2+2x
=>-7x^2-3x+2=0
=>\(x=\dfrac{-3\pm\sqrt{65}}{14}\)
TH2: x<-2
Pt sẽ là \(\dfrac{x}{2x-1}=\dfrac{-3x-2}{-x-2}=\dfrac{3x+2}{x+2}\)
=>6x^2-3x+4x-2=x^2+2x
=>6x^2+x-2=x^2+2x
=>5x^2-x-2=0
mà x<-2
nên \(x\in\varnothing\)